1. 입력 데이터 정규화
딥러닝 모델에 입력되는 데이터는 각기 다른 범위의 값들을 포함할 수 있습니다. 예를 들어, 어떤 특성은 1에서 5 사이의 값을 가질 수 있고, 다른 특성은 1000에서 99999 사이의 값을 가질 수 있습니다. 이러한 데이터를 모델에 직접 입력하면 학습 과정에 부정적인 영향을 미칠 수 있습니다.

위 이미지에서 데이터는 '몸무게'와 '키'라는 두 특성을 갖고 있어요. 몸무게의 단위는 킬로그램(kg)이며, 키의 단위는 센티미터(cm)입니다.
- 왼쪽 표에서 몸무게는 60kg에서 90kg 사이고, 키는 170cm 에서 185cm 사이로 측정되어 있어요. 이러한 데이터를 기계 학습 모델에 직접 적용하면, 더 큰 숫자를 갖는 특성('키')이 모델에 더 큰 영향을 미칠 위험이 있습니다. 모델은 단순히 숫자의 크기 때문에 한 특성을 더 중요하게 여길 수 있고, 그 결과 학습이 왜곡될 수 있는 거죠.
- 오른쪽 표는 몸무게와 키 데이터를 정규화한 결과를 보여줍니다. 정규화는 각 특성의 평균을 0으로, 표준편차를 1로 맞추어줌으로써 모든 특성이 동일한 척도를 갖게 합니다. 오른쪽 표에서는 모든 값이 -1.5부터 1.5 사이로 범위가 좁아졌어요. 결과적으로, 데이터의 모든 특성은 모델 학습에 동등하게 기여할 수 있게 되며, 이는 더 공정하고 균형 잡힌 학습 결과를 가져다줍니다.
이렇게 함으로써 컴퓨터는 특성의 '크기'에 휘둘리지 않고, 각 특성이 제공하는 정보에 더 집중할 수 있어요. 결과적으로, 모델은 각 특성이 가져다주는 진짜 가치를 더 공평하게 평가할 수 있게 됩니다.
2. 정규화가 필요한 이유
즉, 정규화는 모든 입력 특성이 모델에 동일한 중요도로 고려될 수 있도록 보장합니다.
데이터의 특성들이 서로 다른 스케일을 갖고 있을 때, 경사 하강법을 사용한 학습 과정에서 문제가 발생할 수 있습니다. 한 방향의 가중치가 너무 크게 변동하면, 학습 경로가 해당 방향으로 크게 진동하게 되어 최적점에 도달하는 데 더 많은 시간과 단계를 필요로 하게 됩니다.
이러한 경사에서는 한 방향은 매우 가파른 반면 다른 방향은 상대적으로 완만합니다. 가파른 방향으로는 큰 가중치 변경이 이루어지기 쉬워 네트워크가 한쪽 경사면에서 다른 쪽으로 반복해서 움직이는 현상을 경험하게 됩니다. 이는 네트워크가 효율적으로 학습하기 어렵게 만들며, 최적화 과정을 길게 합니다.

반면, 특성들을 같은 스케일로 정규화하면 이러한 문제를 상당 부분 완화할 수 있습니다. 모든 방향이 균일하게 조정되면 손실 경관이 더욱 평탄하고 그릇 모양처럼 되어 경사 하강법이 최적점을 향해 부드럽고 효율적으로 진행될 수 있겠죠~
3. 배치 정규화의 필요성
신경망을 훈련할 때 기본적으로 파라미터(가중치)를 조절하여 출력을 최적화합니다. 이 학습 과정에서 입력값의 작은 변화가 결과에 미치는 영향, 즉 그래디언트를 계산하여 파라미터를 업데이트하게 됩니다. 그러나 이 그래디언트가 너무 작아지거나 (Vanishing) 혹은 너무 커지는 (Exploding) 문제가 발생하면 신경망은 효과적으로 학습할 수 없게 됩니다.

또한, 신경망이 미니배치를 사용해 학습을 진행할 때마다 입력값은 매번 랜덤으로 변경되므로, 이는 학습 과정의 안정성을 저해하고 파라미터 업데이트의 일관성을 떨어뜨릴 수 있습니다. (위 이미지 참고)
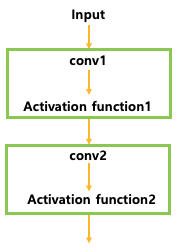
신경망에서 각 은닉층을 고려해 보면, 이전 층의 활성화 값들은 그저 다음 층으로의 입력일 뿐입니다. 예를 들어, 위 그림에서 2번째 층을 보면, 이전 층들을 고려하지 않고 1번째 층에서 온 활성화 값들이 바로 입력이 됩니다.
만약 우리가 각 이전 층의 활성화 값을 어떻게든 정규화할 수 있다면, 학습 중 경사 하강법이 더 잘 수렴할 것입니다.
4. 배치 정규화는 어떻게 작동하나요?
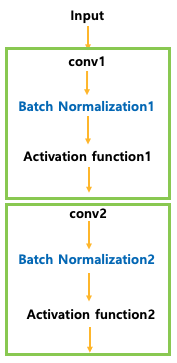
배치 정규화는 네트워크의 은닉층 사이에 삽입되는 또 다른 네트워크 레이어입니다. 이 레이어의 주요 역할은 첫 번째 은닉층에서 나온 출력을 정규화하여 다음 은닉층의 입력으로 전달하는 것입니다.
5. 배치 정규화의 기본 단계
5.1 정규화 단계
먼저, 각 미니배치에 대해 각 특성 \( x^{(k)} \)의 평균 \( \mu_B \)과 분산 \( \sigma_B^2 \)를 계산합니다. 이 평균과 분산을 사용하여, 각 데이터 포인트를 다음과 같이 정규화합니다.
\[ \hat {x}^{(k)} = \frac {x^{(k)} - \mu_B}{\sqrt {\sigma_B^2 + \epsilon}} \]
- \( x^{(k)} \): 입력 특성
- \( \mu_B \): 미니배치 \( B \)에 대한 평균
- \( \sigma_B^2 \): 미니배치 \( B \)에 대한 분산
- \( \epsilon \): 수치적 안정성을 위한 작은 상수 (예: \( 10^{-8} \))
이 단계의 목적은 입력 특성의 분포를 평균 0, 분산 1로 정규화하여, 모델이 더 안정적으로 학습할 수 있도록 하는 것입니다.
5.2 스케일 및 시프트 단계
정규화된 데이터 \( \hat {x}^{(k)} \)는 이제 네트워크가 특정 작업에 더 적합하도록 스케일과 시프트를 조정할 수 있습니다. 이는 다음과 같이 수행됩니다.
\[ y^{(k)} = \gamma \hat {x}^{(k)} + \beta \]
- \( \gamma \): 스케일 파라미터, 학습 가능
- \( \beta \): 시프트 파라미터, 학습 가능
이 단계에서 \( \gamma \)와 \( \beta \)는 학습 과정에서 최적화됩니다. 이 파라미터들은 각 배치 정규화 레이어에서 독립적으로 학습되며, 신경망이 각 레이어에서 최적의 데이터 분포를 학습할 수 있도록 합니다.
5.3 전체 과정: \( g(BN(Wx)) \) 형태의 유도
이제 신경망에서 배치 정규화를 적용하는 전체 과정을 살펴보겠습니다. 신경망의 한 레이어를 예로 들면, 입력 \( x \)에 대해 가중치 \( W \)를 적용한 다음 배치 정규화를 적용하고, 활성화 함수 \( g \)를 적용합니다.
1. 선형 변환: 입력 \( x \)에 대해 선형 변환 \( Wx \)를 수행합니다.
2. 배치 정규화 적용: \( Wx \)에 배치 정규화를 적용합니다.
a) 평균과 분산을 계산
$$ \mu_B = \frac {1}{m} \sum (Wx_i) $$
$$ \sigma_B^2 = \frac {1}{m} \sum ((Wx_i - \mu_B)^2) $$
b) 정규화
$$ \hat {x}^{(k)} = \frac {Wx^{(k)} - \mu_B}{\sqrt {\sigma_B^2 + \epsilon}} $$
c) 스케일 및 시프트
$$ y^{(k)} = \gamma \hat {x}^{(k)} + \beta $$
3. 활성화 함수 적용: 정규화, 스케일, 시프트 된 결과에 활성화 함수 \( g \)를 적용합니다.
\[ z^{(k)} = g(y^{(k)}) = g(\gamma \hat {x}^{(k)} + \beta) \]
최종적으로, 이 모든 과정을 통합하면 신경망의 해당 레이어는 \( g(BN(Wx)) \) 형태로 표현될 수 있습니다. 여기서 \( BN(Wx) \)는 \( Wx \)에 배치 정규화를 적용한 결과입니다.
5.4. 결론
네트워크 레이어의 매개변수인 가중치와 편향과 마찬가지로 배치 정규화 레이어에도 자체적으로 두 종류의 파라미터를 가지는데요. 그것은 바로 베타(β)와 감마(γ)입니다.
이 파라미터들은 각 배치 정규화 레이어에서 학습되며, 신경망이 훈련 데이터에 맞게 조정할 수 있도록 돕습니다. 예를 들어, 네트워크에 세 개의 은닉층과 세 개의 배치 정규화 레이어가 있는 경우, 각 배치 정규화 레이어마다 별도의 베타와 감마 파라미터 세트가 존재합니다.
🎯 위 식에서 편향(b)은 왜 생략했을까?
배치 정규화를 적용할 때, 신경망의 각 레이어에서 입력 \( x \)에 대한 선형 변환은 일반적으로 \( Wx + b \) 형태로 표현됩니다. 여기서 \( W \)는 가중치, \( b \)는 편향입니다. 하지만 배치 정규화를 적용하는 경우, 편향 \( b \)는 다음과 같은 이유로 일반적으로 생략됩니다.
1. 평균 빼기 단계에서의 중복 제거: 배치 정규화에서는 입력의 평균을 빼는 단계가 있습니다. 만약 입력이 \( Wx + b \)라면, 미니배치에 대한 평균 \( \mu_B \)는
\[ \mu_B = \frac {1}{m} \sum_{i=1}^m (Wx_i + b) \]
이 되며, 이를 각 데이터 포인트에서 빼줄 때,
\[ (Wx_i + b) - \mu_B = Wx_i + b - \left(\frac {1}{m} \sum_{j=1}^m Wx_j + b\right) \]
\[ = Wx_i - \frac{1}{m} \sum_{j=1}^m Wx_j \]
로 정리되어, \( b \)는 사라지게 됩니다. 결국 \( Wx \)만이 남게 됩니다.
2. 시프트 파라미터 \( \beta \)의 역할: 배치 정규화에서는 정규화된 데이터에 대해 새로운 시프트 파라미터 \( \beta \)를 도입합니다. 이 \( \beta \)는 학습 가능한 파라미터로, 원래 편향 \( b \)가 가지던 역할을 대체할 수 있습니다. 따라서 원래의 편향 \( b \)는 redundant 하게 되어 필요 없습니다.
따라서, 배치 정규화를 적용하는 과정에서 원래의 편향 \( b \)는 중복된 역할을 하게 되므로 일반적으로 생략되며, \( g(BN(Wx)) \) 형태로 모델을 표현합니다. 이렇게 함으로써, 학습 과정이 더 간단해지고, 편향 \( b \)에 대한 중복 계산을 피할 수 있습니다.
6. 추론 시 배치 정규화의 동작 원리
추론 시에 배치 정규화를 적용하는 방법은 훈련 과정과는 약간 다릅니다. 훈련 시에는 각 미니배치에 대해 평균과 분산을 계산하고 사용하지만, 추론 시에는 고정된 평균과 분산을 사용하여 입력을 정규화합니다. 이 고정된 값들은 일반적으로 훈련 과정 중에 계산된 미니배치의 평균과 분산을 기반으로 계산된 "이동 평균(moving average)"과 "이동 분산(moving variance)"을 통해 얻어집니다.
6.1. 이동 평균 (Moving Average)
이동 평균은 시계열 데이터나 연속적으로 변화하는 데이터에서 사용되는 통계 기법 중 하나로, 데이터의 잡음을 줄이고 실제로 유용한 트렌드를 파악하기 위해 사용됩니다.
\[ \mu_{\text {moving}} = \frac {1}{m} \sum_{i=1}^{m} \mu_{B_i} \]
이동 평균 \( \mu_{\text {moving}} \)은 훈련 과정에서 각 미니배치 \( B_i \)에 대한 평균 \( \mu_{B_i} \)의 평균을 계산하는 방식으로 정의됩니다. 즉, \( m \) 개의 미니배치에서 각각 계산된 평균들의 평균을 취하는 것입니다. 이를 통해 얻은 \( \mu_{\text {moving}} \)는 모델이 추론을 수행할 때 사용되는 평균값으로, 훈련 데이터 전체의 일반적인 특성을 반영하도록 돕습니다.
- \( \mu_{B_i} \): \( i \) 번째 미니배치의 평균
- \( m \): 이동 평균을 계산하는 데 사용된 미니배치의 수
- \( \mu_{\text {moving}} \): 계산된 미니배치 평균들의 평균
6.2. 이동 분산 (Moving Variance)
이동 분산(Moving Variance)은 이동 평균과 비슷한 개념입니다.
\[ \sigma_{\text {moving}}^2 = \frac {1}{m} \sum_{i=1}^{m} \sigma_{B_i}^2 \]
- \( \sigma_{B_i}^2 \): \( i \) 번째 미니배치의 분산
- \( m \): 이동 분산을 계산하는 데 사용된 미니배치의 수
- \( \sigma_{\text {moving}}^2 \): 계산된 미니배치 분산들의 평균
이동 분산의 계산은 각 미니배치의 분산 값을 평균 내어 얻습니다. 이는 훈련 과정 중에 각 미니배치의 데이터 분포가 가지는 변동성을 반영하며, 이러한 분산의 평균값은 모델이 추론을 수행할 때 사용됩니다.
이와 같이 계산된 이동 평균과 이동 분산은 학습이 끝난 후 고정되어 추론 시 사용됩니다.
6.3. 추론 시 정규화
추론 시에는 학습 데이터셋 전체에서 계산된 (또는 이동 평균을 사용하여 계산된) 평균과 분산을 사용하여 입력을 정규화합니다. 추론 시 정규화된 입력 \( \hat {x} \)는 다음과 같이 계산됩니다.
\[ \hat {x}^{(k)} = \frac {x^{(k)} - \mu_{\text {moving}}}{\sqrt {\sigma_{\text {moving}}^2 + \epsilon}} \]
- \( x^{(k)} \): 추론하려는 입력 데이터.
- \( \mu_{\text {moving}} \): 학습 시 계산된 이동 평균.
- \( \sigma_{\text {moving}}^2 \): 학습 시 계산된 이동 분산.
- \( \epsilon \): 수치적 안정성을 위한 작은 상수.
6.4. 추론 시 스케일 및 시프트 적용
정규화된 데이터에 학습된 스케일 파라미터 \( \gamma \)와 시프트 파라미터 \( \beta \)를 적용합니다.
\[ y^{(k)} = \gamma \hat {x}^{(k)} + \beta \]
- \( \gamma \): 학습 과정에서 얻은 스케일 파라미터.
- \( \beta \): 학습 과정에서 얻은 시프트 파라미터.
6.4. 결론
추론 시에 배치 정규화는 학습 시에 미니배치로부터 얻은 이동 평균과 이동 분산을 사용하여 입력 데이터를 정규화합니다. 이를 통해 모델이 학습 과정에서 보았던 비슷한 데이터 분포를 기반으로 새로운 데이터에 대해 일관되고 안정적인 예측을 수행할 수 있습니다.
🎯 이동 평균? 이동 분산?
이동 평균(moving average)은 시간이나 다른 차원에 따라 연속적으로 계산된 평균값들을 부드럽게 만드는 방법입니다. 특히 배치 정규화에서의 이동 평균은 학습 과정에서 각 미니배치에 대한 평균과 분산의 평균을 계산하여, 추론 시에 사용하기 위한 전체 데이터셋의 대표적인 통계량을 제공합니다.
배치 정규화에서 이동 평균은 다음과 같이 정의됩니다.
1. 이동 평균 (Moving Average): 이는 각 미니배치에서 계산된 평균들의 평균을 시간이나 순서에 따라 업데이트하는 것입니다. 이를 통해 학습 과정에서 얻은 평균값들을 안정적으로 반영합니다.
2. 이동 분산 (Moving Variance): 이는 각 미니배치에서 계산된 분산들의 평균을 시간이나 순서에 따라 업데이트하는 것입니다. 이를 통해 학습 과정에서 얻은 분산값들을 안정적으로 반영합니다.
이동 평균 \( \mu_{\text {moving}} \)은 다음과 같은 방법으로 계산됩니다:
\[ \mu_{\text {moving}} = (1 - \alpha) \cdot \mu_{\text{moving}} + \alpha \cdot \mu_B \]
- \( \mu_{\text{moving}} \): 이전까지의 이동 평균.
- \( \alpha \): 평활 계수(smoothing coefficient), 일반적으로 0과 1 사이의 값.
- \( \mu_B \): 현재 미니배치의 평균.
이동 평균의 의미
- 학습 과정: 학습 시 각 미니배치의 평균 \( \mu_B \)와 분산 \( \sigma_B^2 \)를 계산하고, 이를 이용해 모델이 각 배치에 대해 정규화된 출력을 생성할 수 있도록 합니다.
- 추론 과정: 학습이 끝난 후, 추론 시에는 각 미니배치의 평균과 분산 대신, 전체 학습 과정에서 계산된 이동 평균 \( \mu_{\text{moving}} \)과 이동 분산 \( \sigma_{\text {moving}}^2 \)을 사용합니다. 이는 학습된 모델이 보았던 전체 데이터의 통계를 대표하는 값으로, 모델이 보다 일관된 데이터 분포를 기반으로 예측을 수행하도록 합니다.
이동 평균의 구체적인 예
예를 들어, 학습 과정에서 3개의 미니배치의 평균이 각각 100, 110, 105라고 할 때, 이동 평균을 계산하는 과정은 다음과 같습니다:
1. 초기 \( \mu_{\text {moving}} = 0 \), \( \alpha = 0.1 \)
2. 첫 번째 미니배치 후: \( \mu_{\text{moving}} = (1 - 0.1) \cdot 0 + 0.1 \cdot 100 = 10 \)
3. 두 번째 미니배치 후: \( \mu_{\text{moving}} = (1 - 0.1) \cdot 10 + 0.1 \cdot 110 = 19 \)
4. 세 번째 미니배치 후: \( \mu_{\text{moving}} = (1 - 0.1) \cdot 19 + 0.1 \cdot 105 = 27.6 \)
이와 같은 방식으로 이동 평균은 각 단계에서 업데이트되며, 학습이 진행될수록 전체 데이터셋의 평균을 더 정확하게 반영하게 됩니다.
'Deep learning' 카테고리의 다른 글
| [Deep Learning] 인공지능의 기초: 퍼셉트론부터 인공 신경망까지 (2) | 2024.02.06 |
|---|---|
| [Deep learning] 가중치 초기화(weight initialization) (feat. Xavier, He,normal, uniform) (1) | 2023.09.06 |
| [Deep learning] 정제와 정규화 (cleaning and normalization) (0) | 2023.03.03 |
| [Deep learning] Callback 함수 (0) | 2023.02.06 |