앞서 TF-IDF (Term Frequency-Inverse Document Frequency)를 사용하여 텍스트 데이터를 벡터화하는 방법을 배웠습니다.
이제, 이 TF-IDF 벡터를 활용하여 문서 간 유사도를 계산해보려 합니다.
텍스트 데이터의 유사도를 측정하는 방법으로는 여러 가지가 있지만, 이번에는 코사인 유사도 (Cosine Similarity), 유클리드 거리 (Euclidean Distance), 그리고 자카드 유사도 (Jaccard Similarity)를 사용하여 영화 추천 시스템을 구축해 보겠습니다.
유클리드 거리 vs 코사인 유사도 vs 자카드 유사도 비교
| 기준 | 유클리드 거리 (Euclidean Distance) |
코사인 유사도 (Cosine Similarity) |
자카드 유사도 (Jaccard Similarity) |
| 측정 방식 | 벡터 간의 직선 거리 | 벡터 간의 각도 | 두 집합 간의 교집합과 합집합 비율 |
| 벡터 크기 영향 | 벡터의 크기에 민감 | 벡터의 크기를 무시하고 방향만 고려 | 벡터의 크기보다는 단어의 존재 여부에 중점 |
| 주요 활용 분야 | 수치 데이터 분석, 좌표 거리 측정 | 텍스트 데이터 분석, 추천 시스템 | 문서 유사도 분석, 검색 엔진 최적화 |
| 스케일링 필요 여부 | 필수 | 불필요 | 불필요 |
| 회소 행렬에서의 성능 | 부정확한 결과 가능 | 상대적으로 효율적 | 공통 단어가 적을 경우 부정확 |
| 문서 길이 영향 | 영향 있음 | 영향 없음 | 영향 없음 (단어의 존재 여부만 반영) |
| 장점 | - 좌표 공간에서의 실제 거리 측정 가능 - 수치 데이터 분석에 유리 |
- 텍스트 데이터에서 문서 길이와 관계없이 유사도 평가 가능 |
- 단어의 존재 여부만으로 유사도 측정 가능 - 빠른 계산 속도 |
| 단점 | - 벡터의 크기에 민감하여 텍스트 데이터에 부적합 - 스케일링 필요 |
- 단어 간 문맥을 고려하지 못함 | - 단어가 희귀할 경우 유사도 평가가 어려움 - 연속형 데이터에는 부적합 |
- 코사인 유사도는 두 벡터 간의 방향을 기준으로 유사도를 측정합니다. 벡터의 크기와 관계없이 방향이 유사할수록 높은 유사도로 평가되기 때문에, 텍스트 데이터나 추천 시스템에서 자주 사용됩니다.
- 유클리드 거리는 두 벡터 간의 직선거리를 측정합니다. 벡터 간의 거리가 가까울수록 두 텍스트가 더 유사하다고 판단합니다. 다만, 벡터의 크기에 영향을 받기 때문에 문서 길이에 따라 왜곡된 결과를 초래할 수 있습니다.
- 자카드 유사도는 두 집합 간의 유사도를 측정하는 방법으로, 공통된 요소의 비율을 기반으로 합니다. 텍스트 데이터를 집합 형태로 변환하여 단어의 중복도를 제거하고, 두 텍스트 간의 공통된 단어 비율을 비교합니다. 이 방법은 텍스트의 내용이 유사하지만 단어 빈도가 다른 경우에도 문서 간의 유사성을 잘 평가할 수 있습니다.
이제, 각 유사도 측정 방법을 활용하여 영화 줄거리 데이터를 분석하고, 사용자가 입력한 영화와 유사한 영화를 추천하는 시스템을 만들어 보겠습니다.
코사인 유사도(Cosine Similarity)란?
코사인 유사도는 두 벡터 간의 각도를 이용해 유사도를 측정하는 방법입니다.
벡터의 크기가 아니라 방향이 얼마나 유사한지를 평가하기 때문에, 텍스트 데이터나 추천 시스템에서 자주 활용됩니다.
\[
\text {Cosine Similarity}(A, B) = \frac {A \cdot B}{\|A\| \|B\|}
\]
- \( A \cdot B \): 두 벡터의 내적
- \( \|A\| \): 벡터 \( A \)의 크기(길이)
- \( \|B\| \): 벡터 \( B \)의 크기(길이)
(문서 단어 행렬이나 TF-IDF 행렬을 통해서 문서의 유사도를 구하는 경우에는 문서 단어 행렬이나 TF-IDF 행렬이 각각의 벡터 A, B가 됩니다.)
코사인 유사도의 값이
- 1에 가까울수록 두 벡터가 유사함을 의미합니다.
- 0에 가까울수록 두 벡터가 서로 직각임을 의미합니다(즉, 유사하지 않음).
- -1에 가까울수록 두 벡터가 반대 방향을 가리킴을 의미합니다(이 경우는 텍스트나 추천 시스템에서 거의 발생하지 않음).
코사인 유사도가 벡터의 크기에 영향을 받지 않는 이유
공식에서 보시다시피, 코사인 유사도는 두 벡터의 내적을 각 벡터의 크기(길이)로 나눕니다.
이 과정을 통해 벡터의 크기를 정규화하게 됩니다.
즉, 벡터의 크기가 아무리 커도 내적 값은 그 크기로 나눠지기 때문에 결과적으로 크기(길이)의 영향을 제거하게 됩니다.
예를 들어,
벡터의 크기가 다른 경우
- 벡터 \( A = [1, 1] \)
- 벡터 \( B = [2, 2] \)
코사인 유사도 계산
\[
A \cdot B = 1 \times 2 + 1 \times 2 = 4
\]
\[
\|A\| = \sqrt {1^2 + 1^2} = \sqrt {2}, \quad \|B\| = \sqrt {2^2 + 2^2} = \sqrt {8}
\]
\[
\text {Cosine Similarity}(A, B) = \frac {4}{\sqrt {2} \times \sqrt {8}} = \frac {4}{4} = 1
\]
결과적으로, 벡터의 크기가 다르지만 방향이 동일하기 때문에 코사인 유사도는 1이 됩니다.
벡터의 방향이 다른 경우
- 벡터 \( A = [1, 0] \)
- 벡터 \( B = [0, 1] \)
코사인 유사도 계산
\[
A \cdot B = 1 \times 0 + 0 \times 1 = 0
\]
\[
\|A\| = \sqrt {1^2 + 0^2} = 1, \quad \|B\| = \sqrt {0^2 + 1^2} = 1
\]
\[
\text {Cosine Similarity}(A, B) = \frac {0}{1 \times 1} = 0
\]
여기서, 벡터의 크기가 같아도 방향이 다르기 때문에 코사인 유사도는 0이 됩니다.
정리하자면,
코사인 유사도는 벡터의 크기를 정규화하기 때문에, 벡터의 길이(크기)에는 영향을 받지 않습니다. 대신, 두 벡터의 방향(각도)에만 초점을 맞추어 유사도를 측정합니다. 따라서 문서의 길이(단어 수)와 관계없이, 내용의 유사성을 더 잘 평가할 수 있습니다.
텍스트 데이터에서 코사인 유사도는 어떻게 계산할까?
예를 들어, 세 개의 문서에 대해 TF-IDF를 계산했다고 가정해 보겠습니다.
1. 문서 1의 TF-IDF 결과: `[0.5, 0.3, 0.0, 0.2]`
2. 문서 2의 TF-IDF 결과: `[0.1, 0.7, 0.0, 0.4]`
3. 문서 3의 TF-IDF 결과: `[0.0, 0.2, 0.6, 0.1]`
TF-IDF 벡터를 사용해 코사인 유사도를 계산하는 과정은 다음과 같습니다.
\[
\text{Cosine Similarity}(A, B) = \frac {A \cdot B}{\|A\| \times \|B\|}
\]
만약, 우리가 문서 1과 문서 2의 코사인 유사도를 계산한다고 가정해 보겠습니다.
- 문서 1의 벡터: `[0.5, 0.3, 0.0, 0.2]`
- 문서 2의 벡터: `[0.1, 0.7, 0.0, 0.4]`
1. 내적 계산 (\( A \cdot B \)):
\[
(0.5 \times 0.1) + (0.3 \times 0.7) + (0.0 \times 0.0) + (0.2 \times 0.4) = 0.05 + 0.21 + 0 + 0.08 = 0.34
\]
2. 벡터의 크기 계산 (\( \|A\| \)와 \( \|B\| \)):
\[
\|A\| = \sqrt {0.5^2 + 0.3^2 + 0.0^2 + 0.2^2} = \sqrt {0.25 + 0.09 + 0 + 0.04} = \sqrt {0.38} \approx 0.616
\]
\[
\|B\| = \sqrt {0.1^2 + 0.7^2 + 0.0^2 + 0.4^2} = \sqrt {0.01 + 0.49 + 0 + 0.16} = \sqrt {0.66} \approx 0.812
\]
3. 코사인 유사도 계산:
\[
\text {Cosine Similarity}(A, B) = \frac {0.34}{0.616 \times 0.812} = \frac {0.34}{0.500} \approx 0.68
\]
코사인 유사도 (Cosine Similarity)의 장단점
장점
- 코사인 유사도는 벡터의 크기(길이)가 아닌 방향에 초점을 맞춰 두 벡터 간의 유사도를 측정하기 때문에 텍스트 데이터에서 문서의 길이와 무관하게 내용의 유사성을 평가할 수 있어, 문서 분류, 추천 시스템 등에 효과적입니다.
- 희소 행렬(Sparse Matrix)에서 0이 많은 경우에도 유사도를 측정하는 데 있어 유클리드 거리보다 더 정확한 결과를 제공합니다.
- 코사인 유사도는 벡터의 방향만 고려하므로, 벡터의 크기에 영향을 받지 않습니다. 따라서 정규화 과정 없이 바로 유사도를 계산할 수 있어 계산 비용을 줄일 수 있습니다.
- 추천 시스템, 문서 검색, 클러스터링 등에서 문서 간의 내용 유사성을 평가할 때 자주 사용됩니다. 특히 텍스트 데이터와 같이 벡터의 크기보다는 단어의 조합과 빈도가 중요한 경우에 유리합니다.
단점
- 코사인 유사도는 단순히 단어의 빈도와 중요도만을 사용하여 벡터를 비교하기 때문에, 단어 간의 문맥적 관계를 고려하지 못합니다. 예를 들어, 동의어나 유사한 의미를 가진 단어가 다른 벡터로 표현되면, 문서의 의미가 유사하더라도 낮은 유사도 값을 가질 수 있습니다.
예를 들어, "car"와 "vehicle"이 동의어이더라도, "car"가 한 문서에서 자주 등장해 TF-IDF 값이 낮고, "vehicle"이 다른 문서에서 드물게 등장해 TF-IDF 값이 높다면, 두 벡터는 다른 방향을 가질 수 있습니다. 이로 인해 코사인 유사도 값이 낮게 나오게 되는 거죠. 이를 해결하기 위해 Word2Vec, BERT와 같은 임베딩 기법을 활용하면 단어 간의 문맥을 반영하여 더 정확한 유사도 측정이 가능합니다.
- 희소 행렬에서 공통으로 등장하는 단어가 거의 없는 경우, 대부분의 값이 0이 됩니다. 예를 들어, 'car'라는 단어가 문서 1에만 1번 등장하고 다른 문서에는 전혀 등장하지 않는다면, 다른 문서에서는 해당 단어의 값이 모두 0이 됩니다. 이로 인해 문서 간 유사도를 비교할 때 코사인 유사도가 낮게 나올 수 있습니다.
- 단어의 순서를 무시하고 벡터화된 단어 빈도만을 사용하기 때문에 문장의 구조나 문맥을 반영하지 못해, 같은 단어들이 포함되어 있어도 다른 의미를 가질 수 있는 문장들을 구분하지 못합니다.
결론적으로, 코사인 유사도는 텍스트 데이터에서 문서의 길이에 영향을 받지 않고 유사도를 측정할 수 있어, 추천 시스템과 텍스트 분류 등에 매우 적합하지만, 단어의 순서나 문맥을 고려하지 않기 때문에, 더 깊은 의미를 이해하는 데 한계가 있습니다.
따라서 코사인 유사도는 텍스트 데이터에서 주로 사용되지만, 더 높은 수준의 이해가 필요한 분석에서는 Word2Vec, BERT와 같은 임베딩 기법을 사용할 수도 있습니다.
코사인 유사도를 이용한 텍스트 문서 유사도 분석 (예제)
우리가 앞서 학습한 TF-IDF를 이용해 문서를 벡터로 변환한 후, 코사인 유사도를 통해 문서 간 유사도를 측정해 보겠습니다.
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
import pandas as pd
# 예제 문서 리스트
corpus = [
"나는 오늘 밥을 먹었다",
"밥을 먹고 운동을 했다",
"오늘 운동을 마치고 밥을 먹었다"
]
# TF-IDF 벡터화
vectorizer = TfidfVectorizer()
tfidf_matrix = vectorizer.fit_transform(corpus)
# 코사인 유사도 계산
cosine_sim = cosine_similarity(tfidf_matrix, tfidf_matrix)
# 결과를 데이터프레임으로 보기 좋게 출력
df = pd.DataFrame(cosine_sim, index=["문서1", "문서2", "문서3"], columns=["문서1", "문서2", "문서3"])
print("코사인 유사도 행렬:")
print(df)
문서 1, 2, 3의 코사인 유사도 결과를 보면,
문서 1과 문서 3의 유사도가 0.552로 가장 높습니다. 이는 두 문서에 유사한 단어가 많이 포함되어 있다는 것을 의미합니다.
또한 문서 2와 다른 문서들 간의 유사도는 상대적으로 낮습니다.
코사인 유사도를 이용한 영화 추천 시스템 (실습)
추천 시스템이란?
- 추천 시스템은 사용자의 취향을 분석하여 관련된 콘텐츠(예: 영화, 음악, 도서)를 추천하는 시스템입니다.
- 콘텐츠 기반 추천과 협업 필터링 추천 방식이 대표적입니다.
이제 코사인 유사도를 활용하여,
좋아하는 영화를 입력하면 해당 영화의 줄거리와 유사한 줄거리의 영화를 찾아서 추천하는 코드를 작성해 보도록 해요.
우선 사용할 데이터셋을 불러옵니다.
import pandas as pd
# 인코딩을 'ISO-8859-1'로 지정하여 파일 로드
movies_df = pd.read_csv('movies_metadata_low.csv', encoding='ISO-8859-1')
`movies_metadata_low.csv` 파일에는 24개의 열(column)과 45466개의 행(row)이 포함되어 있습니다.
사용할 칼럼만 불러와서 확인해 볼게요.
movies_df[['title','overview']]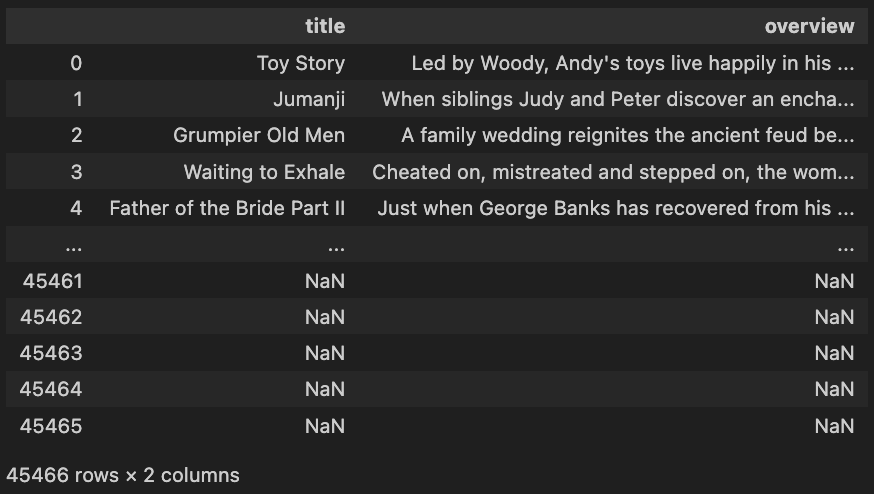
title과 overview 칼럼에는 결측값이 존재하네요.
이제 `overview`(줄거리 설명)을 활용해, 영화 간 유사도를 측정하고 추천 시스템을 구축할 수 있습니다.
1️⃣ 데이터 전처리: overview 열에 결측치 처리 및 텍스트 전처리를 합니다.
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
# Step 1: 결측치 처리 (overview 열에서 결측값을 빈 문자열로 대체)
movies_df['overview'] = movies_df['overview'].fillna('')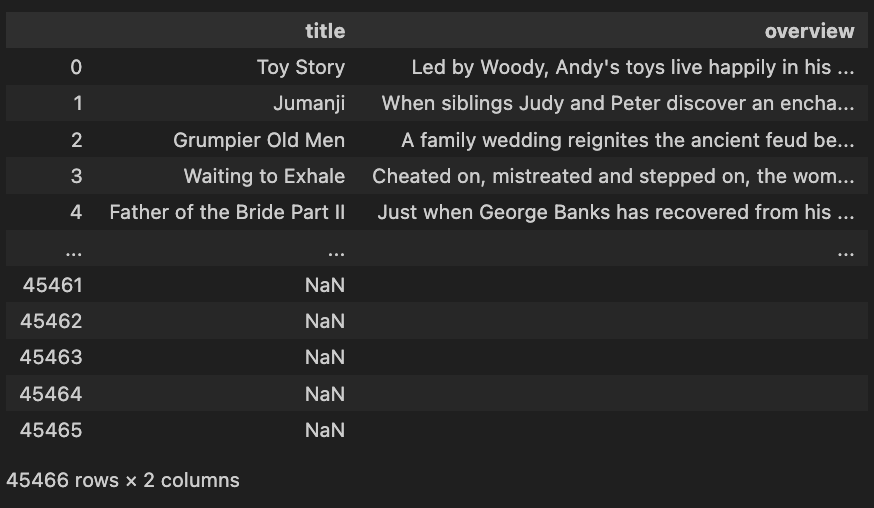
2️⃣ TF-IDF 벡터화: overview 텍스트를 TF-IDF 벡터화하여 문서를 수치화합니다.
# Step 2: TF-IDF 벡터화 (overview 텍스트를 수치화)
tfidf_vectorizer = TfidfVectorizer(stop_words='english')
tfidf_matrix = tfidf_vectorizer.fit_transform(movies_df['overview'])
# TF-IDF 행렬을 Pandas DataFrame으로 변환
tfidf_df = pd.DataFrame(tfidf_matrix.toarray(), columns=tfidf_vectorizer.get_feature_names_out())
print(tfidf_df)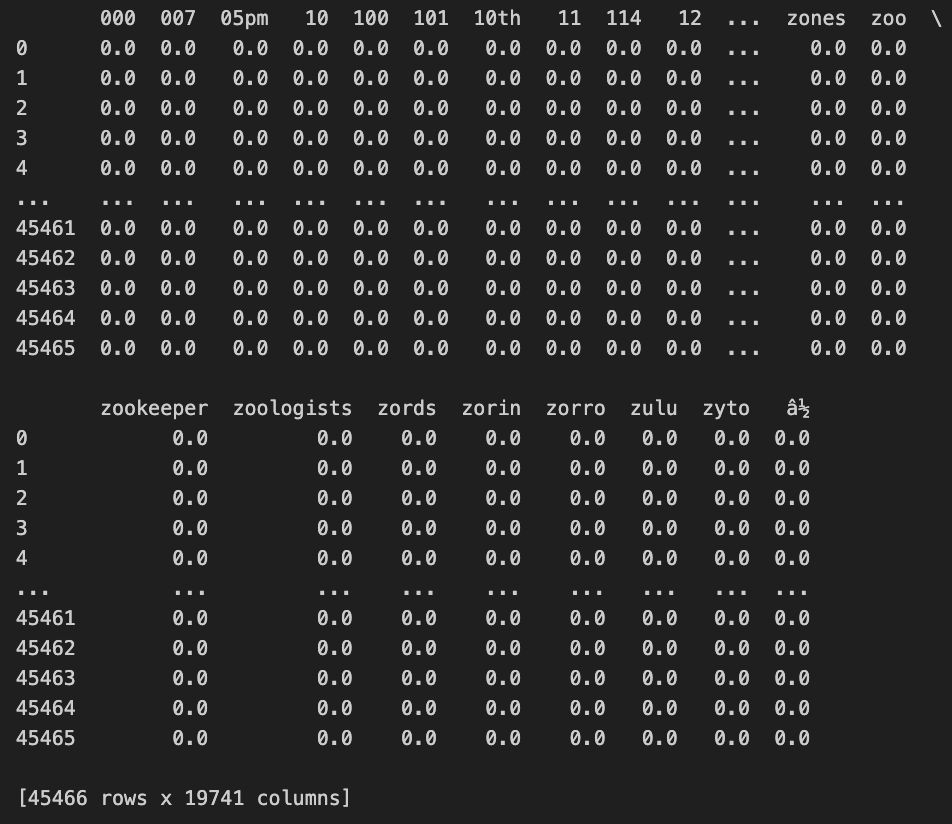
TF-IDF 벡터화한 결과를 보면 총 45466개의 행(row)과 19741개의 열(column)이 출력되었습니다.
이는 45466개의 영화가 있으며, 19741개의 고유한 단어들을 나타냅니다.
3️⃣ 코사인 유사도 계산: 영화 줄거리 간의 코사인 유사도를 계산하여, 특정 영화와 유사한 영화를 찾습니다.
# Step 3: 코사인 유사도 계산 (모든 영화 간의 유사도)
cosine_sim = cosine_similarity(tfidf_matrix, tfidf_matrix)
print('코사인 유사도 연산 결과 :',cosine_sim.shape)
> 코사인 유사도 연산 결과 : (45466, 45466)코사인 유사도 연산 결과로 생성된 행렬은 45466개의 행과 열을 가지고 있습니다.
이는 45466개의 각 문서 벡터(영화 줄거리 벡터)와 자기 자신을 포함한 다른 45466개의 문서 벡터 간의 유사도를 기록한 행렬입니다. 이 행렬에는 모든 영화 간의 상호 유사도가 기록되어 있습니다.
이제 기존 데이터프레임으로부터 영화의 타이틀을 key, 영화의 인덱스를 value로 하는 딕셔너리 movie_indices를 만들어둡니다.
# 영화 제목을 키(key)로, 데이터프레임의 인덱스를 값(value)으로 갖는 딕셔너리 생성
movie_indices = dict(zip(movies_df['title'], movies_df.index))
movie_indices
> {'Toy Story': 0,
'Jumanji': 1,
'Grumpier Old Men': 2,
'Waiting to Exhale': 3,
'Father of the Bride Part II': 4,
'Heat': 5,
'Sabrina': 888,
'Tom and Huck': 7,
'Sudden Death': 8,
'GoldenEye': 9,
'The American President': 10,
'Dracula: Dead and Loving It': 11,
'Balto': 12,
'Nixon': 13,
'Cutthroat Island': 14,
'Casino': 15,
'Sense and Sensibility': 16,
'Four Rooms': 17,
'Ace Ventura: When Nature Calls': 18,
'Money Train': 19,
'Get Shorty': 20,
'Copycat': 21,
'Assassins': 22,
'Powder': 23,
'Leaving Las Vegas': 24,
...
'Robin Hood: Prince of Thieves': 998,
'Mary Poppins': 999,
'Dumbo': 1000,
"Pete's Dragon": 1001,
...}
4️⃣ 추천 시스템 구현: 영화의 제목을 입력하면 사용자가 선택한 영화와 가장 유사한 영화 5개를 추천합니다.
# 코사인 유사도를 기반으로 영화 추천 함수 정의
def get_recommendations(title, cosine_sim=cosine_sim):
# 선택한 영화의 인덱스 가져오기
idx = movie_indices.get(title) # 주어진 영화 제목(title)에 해당하는 인덱스(idx) 값을 반환합니다. ex) 485
if idx is None:
return "해당 영화 제목이 데이터에 없습니다."
# 해당 영화와 다른 영화 간의 유사도 점수 추출
sim_scores = list(enumerate(cosine_sim[idx])) # (영화 인덱스, 유사도 점수) -> [(0, 0.143), (1, 0.0)...]
# 유사도 점수를 기준으로 정렬 (내림차순)
sim_scores = sorted(sim_scores, key=lambda x: x[1], reverse=True)
# 가장 유사한 영화 5개 선택 (자기 자신 제외)
sim_scores = sim_scores[1:6] # [(0, 0.14393405169022885), (959, 0.13863297484628673), (2371, 0.13518346539986825), (3201, 0.12138975288943879), (2845, 0.1172780131667607)]
# 추천 영화 목록 출력
recommended_indices = [i[0] for i in sim_scores] # 영화 인덱스
recommended_titles = movies_df['title'].iloc[recommended_indices] # 영화 제목
return recommended_titles.tolist()
# 예시: 'Malice'와 유사한 영화 추천
get_recommendations("Malice")
> ['Toy Story', 'Bliss', 'Tinseltown', 'Judy Berlin', 'The Story of Us']유클리드 거리 (Euclidean Distance)란?
유클리드 거리는 두 벡터 간의 직선거리를 의미합니다.
값이 작을수록 두 문서가 더 유사하다는 의미이며, 반대로 값이 클수록 문서 간의 차이가 크다는 의미입니다.
주로 좌표 공간에서 두 점 사이의 거리를 구할 때 사용됩니다.
\[
\text {Euclidean Distance}(A, B) = \sqrt {\sum_{i=1}^{n} (A_i - B_i)^2}
\]
- \( A \)와 \( B \): 두 벡터
- \( n \): 벡터의 차원 수
- \( A_i, B_i \): 두 벡터의 각 성분
TF-IDF 벡터화를 통해 각 문서는 수치화된 벡터로 변환됩니다.
각 벡터는 단어의 중요도를 반영한 값들로 구성되어 있으며, 단어마다 다른 TF-IDF 점수를 가집니다.
예를 들어, 두 문서가 비슷한 내용을 가지고 있다면, 이 두 문서의 TF-IDF 벡터는 비슷한 값들을 갖게 되죠.
거리 계산은 다음과 같이 이루어지는데요.
\[
\text {Euclidean Distance}(A, B) = \sqrt {\sum_{i=1}^{n} (A_i - B_i)^2}
\]
여기서 \(A_i\)와 \(B_i\)는 두 문서의 TF-IDF 벡터에서 각 단어의 중요도를 나타내는 값입니다.
TF-IDF 값이 비슷한 문서들은, 위 식에서 각 성분의 차이 \((A_i - B_i)\)가 작아지므로, 유클리드 거리 값이 작게 나오겠죠.
만약, 아래와 같은 3개의 문서가 있는 경우
- 문서 A: "고양이가 귀엽다"
- 문서 B: "고양이가 매우 귀엽다"
- 문서 C: "자동차를 운전하다"
TF-IDF로 벡터화하면 문서 A와 B는 비슷한 단어를 사용하므로 유사한 벡터를 가질 것입니다.
반면, 문서 C는 전혀 다른 단어를 사용하므로 벡터가 다를 것입니다.
결국 유클리드 거리 계산 결과는,
A와 B 간의 거리는 짧고 (비슷한 문서)
A와 C 또는 B와 C 간의 거리는 길어집니다. (내용이 다른 문서)
텍스트 데이터에서 유클리드 거리를 어떻게 계산할까?
예를 들어, 세 개의 문서에 대해 TF-IDF를 계산했다고 가정해 보겠습니다.
1. 문서 1의 TF-IDF 결과: `[0.5, 0.3, 0.0, 0.2]`
2. 문서 2의 TF-IDF 결과: `[0.1, 0.7, 0.0, 0.4]`
3. 문서 3의 TF-IDF 결과: `[0.0, 0.2, 0.6, 0.1]`
TF-IDF 벡터를 사용해 유클리드 거리를 계산하는 과정은 다음과 같습니다.
\[
\text{Euclidean Distance}(A, B) = \sqrt{\sum_{i=1}^{n} (A_i - B_i)^2}
\]
만약, 문서 1과 문서 2의 유클리드 거리를 계산한다면
- 문서 1의 벡터: `[0.5, 0.3, 0.0, 0.2]`
- 문서 2의 벡터: `[0.1, 0.7, 0.0, 0.4]`
1. 벡터 성분 간의 차이 계산
\[
(0.5 - 0.1)^2 = 0.16
\]
\[
(0.3 - 0.7)^2 = 0.16
\]
\[
(0.0 - 0.0)^2 = 0
\]
\[
(0.2 - 0.4)^2 = 0.04
\]
2. 차이 제곱합 계산
\[
0.16 + 0.16 + 0 + 0.04 = 0.36
\]
#### 3. 제곱근 계산
\[
\sqrt {0.36} = 0.6
\]
따라서, 문서 1과 문서 2의 유클리드 거리는 0.6입니다.
유클리드 거리 (Euclidean Distance)의 장단점
장점
- 두 벡터 간의 직선거리를 측정하기 때문에 개념적으로 매우 직관적입니다. 좌표 공간에서 두 점 사이의 거리와 동일한 방식으로 계산되므로, 수치화된 데이터를 분석할 때 쉽게 적용할 수 있습니다.
- 수치형 데이터나 좌표 공간에서의 거리 측정에 적합합니다. 예를 들어, 고객의 위치, 제품의 특징 벡터 등 수치형 데이터를 다룰 때 유용합니다.
- 벡터의 각 성분 간 차이를 고려하기 때문에, 데이터 간의 절대적인 차이를 반영하는 데 유리합니다. 이로 인해 벡터의 크기가 중요한 분석에서 유클리드 거리가 효과적입니다.
단점
- 텍스트 데이터의 경우, 유클리드 거리는 벡터의 크기에 영향을 받습니다. 즉, 문서가 길어지면 해당 벡터의 크기도 커지므로, 두 문서 간의 거리가 실제 유사성과 관계없이 멀어질 수 있습니다. 따라서 문서 길이가 다를 경우, 유클리드 거리는 왜곡된 결과를 초래할 수 있습니다.
- 데이터의 스케일에 매우 민감합니다. 데이터의 범위가 다를 경우, 큰 값이 작은 값보다 더 큰 영향을 미치게 되므로, 데이터를 스케일링(정규화) 하지 않으면 부정확한 결과를 가져올 수 있습니다. (TfidfVectorizer는 정규화를 포함하고 있어서 적용하지 않아도 됨)
- 텍스트 데이터를 TF-IDF로 변환하면, 보통 희소 행렬(Sparse Matrix) 형태로 나타나게 됩니다. 희소 행렬에서 0이 많은 경우, 벡터 성분 간의 차이 값이 커질 수 있어 왜곡된 거리를 초래할 수 있습니다.
- 유클리드 거리는 벡터의 크기 차이만을 반영하기 때문에 텍스트 데이터처럼 벡터의 방향(내용의 유사성)이 중요한 경우에는 부적합할 수 있습니다. 예를 들어, 문서의 길이가 다르지만 내용이 유사한 문서들 간의 유사도를 정확히 평가하기 어렵습니다.
유클리드 거리를 이용한 텍스트 문서 유사도 분석 (예제)
TF-IDF로 벡터화한 문서 데이터를 활용해 유클리드 거리를 계산하고, 문서 간 유사도를 측정해 보겠습니다.
1️⃣ 예제 데이터 준비
from sklearn.feature_extraction.text import TfidfVectorizer
import pandas as pd
from scipy.spatial.distance import euclidean
# 예제 문서 리스트
corpus = [
"나는 오늘 밥을 먹었다",
"밥을 먹고 운동을 했다",
"오늘 운동을 마치고 밥을 먹었다"
]
# TF-IDF 벡터화
vectorizer = TfidfVectorizer()
tfidf_matrix = vectorizer.fit_transform(corpus).toarray()
# 문서 간 유클리드 거리 계산
def calculate_euclidean_distance(matrix):
n = matrix.shape[0] # 문서의 개수
distances = pd.DataFrame(index=range(n), columns=range(n)) # n x n 크기의 빈 데이터프레임 생성
# 문서 간 유클리드 거리 계산
for i in range(n):
for j in range(n):
distances.iloc[i, j] = euclidean(matrix[i], matrix[j])
return distances
# 유클리드 거리 행렬 출력
euclidean_distances = calculate_euclidean_distance(tfidf_matrix)
euclidean_distances.index = ["문서1", "문서2", "문서3"]
euclidean_distances.columns = ["문서1", "문서2", "문서3"]
print("\n유클리드 거리 행렬:")
print(euclidean_distances)
문서 1, 2, 3의 유클리드 거리 결과를 보면,
1. 문서 1과 문서 3의 유클리드 거리가 0.96으로 가장 가깝습니다. 즉, 이 두 문서는 서로 가장 유사한 내용을 가지고 있습니다.
2. 문서 1과 문서 2의 거리는 1.32로, 서로 더 멀리 떨어져 있어 덜 유사합니다.
3. 문서 2와 문서 3의 거리는 1.18입니다. 이 값은 문서 1과 문서 2의 거리보다는 가깝지만, 문서 1과 문서 3만큼 가깝지는 않습니다.
4. 자기 자신과의 거리는 항상 0입니다.
결론적으로
• 문서1과 문서 3이 가장 유사하며,
• 문서1과 문서 2는 가장 덜 유사합니다.
유클리드 거리를 이용한 영화 추천 시스템 (실습)
이제 영화 데이터셋을 활용하여, 영화 줄거리(overview)를 유클리드 거리로 비교해 유사한 영화를 추천하는 시스템을 구축해 보겠습니다.
1️⃣ 데이터 준비 및 전처리
전처리까지는 위에서 진행한 코사인 유사도와 동일한 코드입니다.
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer
from scipy.spatial.distance import euclidean
# 데이터 로드 및 전처리
movies_df = pd.read_csv('movies_metadata_low.csv', encoding='ISO-8859-1')
movies_df['overview'] = movies_df['overview'].fillna('')
# TF-IDF 벡터화
tfidf_vectorizer = TfidfVectorizer(stop_words='english')
tfidf_matrix = tfidf_vectorizer.fit_transform(movies_df['overview']).toarray()
# 영화 제목과 인덱스를 매핑하는 딕셔너리 생성
movie_indices = dict(zip(movies_df['title'], movies_df.index))
2️⃣ 유클리드 거리 기반 추천 함수 구현
def get_recommendations_euclidean(title, n_recommendations=5):
# 선택한 영화의 인덱스 가져오기
idx = movie_indices.get(title)
if idx is None:
return "해당 영화 제목이 데이터에 없습니다."
# 선택한 영화의 TF-IDF 벡터
target_vector = tfidf_matrix[idx]
# 모든 영화와의 유클리드 거리 계산
distances = []
for i in range(len(tfidf_matrix)):
# 선택된 영화(target_vector)와 모든 영화 간의 유클리드 거리를 계산
dist = euclidean(target_vector, tfidf_matrix[i])
distances.append((i, dist))
# 거리 기준으로 정렬 (가까운 순)
distances = sorted(distances, key=lambda x: x[1])
# 가장 가까운 영화 n개 선택 (자기 자신 제외)
recommended_indices = [i[0] for i in distances[1:n_recommendations + 1]]
recommended_titles = movies_df['title'].iloc[recommended_indices]
return recommended_titles.tolist()
# 예시: 'Malice'와 유사한 영화 추천
print(get_recommendations_euclidean("Malice"))
> ['Wings of Courage', 'Roommates', 'Peanuts Die Bank zahlt alles', 'Happy Weekend', 'The Superwife']
자카드 유사도(Jaccard Similarity)란?
자카드 유사도는 두 집합 간의 유사도를 측정하는 지표로, 두 집합의 교집합 크기를 합집합 크기로 나눈 값으로 정의됩니다.
\[
\text {Jaccard Similarity}(A, B) = \frac {|A \cap B|}{|A \cup B|}
\]
- \(A\), \(B\): 비교하고자 하는 두 개의 집합
- \(|A \cap B|\): 두 집합의 교집합 크기
- \(|A \cup B|\): 두 집합의 합집합 크기
자카드 유사도 값은 0부터 1 사이의 값을 가집니다.
- 1에 가까울수록 두 집합이 유사함을 의미합니다.
- 0에 가까울수록 두 집합이 겹치는 부분이 거의 없음을 의미합니다.
텍스트 데이터에서 자카드 유사도(Jaccard Similarity)는 어떻게 계산할까?
아래와 같은 세 개의 문서가 있습니다.
1. 문서 1: "나는 오늘 밥을 먹었다"
2. 문서 2: "밥을 먹고 운동을 했다"
3. 문서 3: "오늘 운동을 마치고 밥을 먹었다"
1. 문서의 토큰화 (단어 집합 생성)
우선, 각 문서를 단어 단위로 분리하여 집합으로 만듭니다.
- 문서 1의 집합: `{나는, 오늘, 밥을, 먹었다}`
- 문서 2의 집합: `{밥을, 먹고, 운동을, 했다}`
- 문서 3의 집합: `{오늘, 운동을, 마치고, 밥을, 먹었다}`
2. 자카드 유사도 계산
문서 1과 문서 2의 자카드 유사도
- 교집합 (\( A \cap B \)): `{밥을}`
- 합집합 (\( A \cup B \)): `{나는, 오늘, 밥을, 먹었다, 먹고, 운동을, 했다}`
\[
\text{Jaccard Similarity}(A, B) = \frac{|A \cap B|}{|A \cup B|} = \frac {1}{7} \approx 0.143
\]
자카드 유사도(Jaccard Similarity)의 장단점
장점
- 집합 간의 유사도를 단순히 교집합과 합집합의 비율로 측정하기 때문에 이해하기 쉽고 계산이 간단합니다.
- 단어의 존재 여부에만 초점을 맞추므로, 이진 데이터(존재/부재)를 분석할 때 유용합니다. 예를 들어, 검색 엔진, 추천 시스템 등에서 주로 사용됩니다.
- 빈도나 가중치 대신 단어의 존재 여부만 고려하기 때문에, 단어 빈도 차이로 인한 영향이 적고, 노이즈에 강합니다.
단점
- 단어의 빈도나 중요도를 반영하지 않기 때문에, 문서에서 단어가 얼마나 중요한지를 고려하지 못합니다. 즉, 단어가 여러 번 등장하더라도 단순히 한 번 존재하는 것과 동일하게 취급됩니다.
- 단어의 문맥적 의미를 반영하지 못합니다. 따라서 동의어나 유사한 의미를 가진 단어가 포함된 문서들이 실제로는 유사하더라도, 낮은 유사도 값을 가질 수 있습니다. 예를 들어, "car"와 "vehicle"이 각각 다른 문서에 포함된 경우, 자카드 유사도는 두 문서를 낮은 유사도로 평가할 수 있습니다.
- 텍스트 데이터를 자카드 유사도로 비교할 때, 공통된 단어가 거의 없는 희소 행렬에서 유사도가 낮게 나옵니다. 특히, 단어가 많고 문서 간에 공통 단어가 적을수록 유사도가 낮아질 수 있어 정확한 유사도 측정이 어려워집니다.
- 단어 수가 매우 적은 짧은 문서 간의 유사도 계산 시, 한 단어의 차이로도 유사도 값이 크게 변동할 수 있습니다.
결론적으로, 자카드 유사도는 단어의 존재 여부를 기준으로 간단하게 유사도를 측정할 수 있는 방법이지만, 단어의 빈도, 중요도, 문맥적 의미를 반영하지 못합니다. 특히, 희소한 데이터나 짧은 문서를 비교할 때는 신뢰도가 낮아질 수 있습니다. 이러한 이유로, 자카드 유사도는 텍스트 데이터 분석보다는 이진 데이터 분석에 더 적합한 경우가 많습니다.
자카드 유사도를 이용한 텍스트 문서 유사도 분석 (예제)
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.metrics import jaccard_score
# 예제 문서 리스트
corpus = [
"나는 오늘 밥을 먹었다",
"밥을 먹고 운동을 했다",
"오늘 운동을 마치고 밥을 먹었다"
]
# CountVectorizer를 사용해 단어 집합 생성 (1-gram 기준)
vectorizer = CountVectorizer()
binary_matrix = vectorizer.fit_transform(corpus).toarray()
# 자카드 유사도 계산
def calculate_jaccard_similarity(matrix):
n = matrix.shape[0]
similarities = []
for i in range(n):
for j in range(i + 1, n):
sim = jaccard_score(matrix[i], matrix[j], average='binary')
similarities.append((f"문서 {i + 1}", f"문서 {j + 1}", sim))
return similarities
# 결과 출력
jaccard_similarities = calculate_jaccard_similarity(binary_matrix)
for doc1, doc2, sim in jaccard_similarities:
print(f"{doc1}와 {doc2}의 자카드 유사도: {sim:.3f}")
문서 1과 문서 3의 자카드 유사도(0.500)가 가장 높습니다. 즉, 문서 1과 문서 3이 다른 문서 쌍에 비해 공통된 단어를 더 많이 가지고 있어서 가장 유사한 것으로 해석할 수 있습니다.
자카드 유사도를 이용한 영화 추천 시스템 (실습)
이제 영화 데이터셋을 활용하여, 영화 줄거리(overview)를 자카드 유사도로 비교해 유사한 영화를 추천하는 시스템을 구축해 보겠습니다.
자카드 유사도를 텍스트 데이터에 적용하려면, 먼저 TF-IDF 대신 이진 벡터를 사용해야 합니다.
`CountVectorizer`를 이용해 이진 벡터로 변환한 후 자카드 유사도를 계산할 수 있습니다.
(CountVectorizer(binary=True)를 사용하여 텍스트를 이진 벡터화합니다. 각 단어가 문서에 존재하면 1, 없으면 0으로 표시합니다.)
import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.metrics import jaccard_score
# 데이터 로드 및 전처리
movies_df = pd.read_csv('movies_metadata_low.csv', encoding='ISO-8859-1')
movies_df['overview'] = movies_df['overview'].fillna('')
# CountVectorizer를 사용해 이진 벡터화
count_vectorizer = CountVectorizer(stop_words='english', binary=True)
binary_matrix = count_vectorizer.fit_transform(movies_df['overview']).toarray()
# 영화 제목과 인덱스를 매핑하는 딕셔너리 생성
movie_indices = dict(zip(movies_df['title'], movies_df.index))
def get_recommendations_jaccard(title, n_recommendations=5):
# 선택한 영화의 인덱스 가져오기
idx = movie_indices.get(title)
if idx is None:
return "해당 영화 제목이 데이터에 없습니다."
# 선택한 영화의 이진 벡터 가져오기
target_vector = binary_matrix[idx]
# 모든 영화와의 자카드 유사도 계산
similarities = []
for i in range(len(binary_matrix)):
sim = jaccard_score(target_vector, binary_matrix[i])
similarities.append((i, sim))
# 유사도 기준으로 정렬 (내림차순)
similarities = sorted(similarities, key=lambda x: x[1], reverse=True)
# 가장 유사한 영화 n개 선택 (자기 자신 제외)
recommended_indices = [i[0] for i in similarities[1:n_recommendations + 1]]
recommended_titles = movies_df['title'].iloc[recommended_indices]
return recommended_titles.tolist()
# 'Malice'와 유사한 영화 추천
print(get_recommendations_jaccard("Malice"))
> ['Bliss', 'The Story of Us', 'Judy Berlin', 'American Graffiti', 'In Dreams']
'pytorch' 카테고리의 다른 글
| [pytorch] 시퀀스-투-시퀀스(seq2seq) (1) | 2024.12.31 |
|---|---|
| [pytorch] DTM과 TF-IDF | 텍스트 전처리 | 자연어 처리 (0) | 2024.11.22 |
| [pytorch] Bag of Words (BOW) | CountVectorizer (0) | 2024.11.19 |
| [pytorch] 정수 인코딩(Integer Encoding) | Counter 와 FreqDist를 활용한 정수 인코딩 코드 (2) | 2024.11.14 |
| [pytorch] 정규 표현식(Regular Expression) | 특수 문자(metacharacters)| 모듈 함수 (module functions) | 정규 표현식을 이용한 토큰화 (RegexpTokenizer) (0) | 2024.11.13 |