Feature Scaling이란?
Feature Scaling은 데이터의 피처(feature)들이 서로 다른 범위(scale)를 가질 때 이를 동일한 스케일로 맞추는 작업입니다. 서로 다른 스케일을 가진 데이터들은 모델의 성능을 떨어뜨리기 때문에 중요한 기법입니다.
Feature Scaling의 효과 4가지
- 알고리즘의 민감도 감소: 대부분의 머신러닝 알고리즘은 피처 값의 크기와 단위에 민감합니다. 예를 들어, 유클리디안 거리 기반 알고리즘(KNN, SVM 등)은 피처 값의 스케일에 큰 영향을 받습니다. 피처 값의 크기 차이가 크면 특정 피처가 모델에 과도한 영향을 미칠 수 있습니다.
- 학습 속도 향상: 경사 하강법을 사용하는 알고리즘(선형 회귀, 로지스틱 회귀, 신경망 등)은 피처 값의 크기에 따라 학습 속도가 달라집니다. 스케일링을 통해 경사 하강법의 수렴 속도를 개선할 수 있습니다
- 모델 성능 개선: 피처 값이 스케일링되지 않은 경우, 모델의 예측 성능이 저하될 수 있습니다. 피처 스케일링을 통해 모델의 성능을 향상할 수 있습니다
- 공정한 피처 반영: 모든 피처가 동등하게 모델에 반영되도록 하여, 특정 피처의 중요도가 과도하게 부각되는 것을 방지합니다.
feature scaling이 필요한 주요 알고리즘
Feature scaling은 알고리즘이 피처의 크기와 단위에 민감할 때 중요합니다. 다음은 feature scaling이 필요한 주요 알고리즘들입니다.
✅ 경사 하강법 기반 알고리즘 (Gradient Descent-based Algorithms)
선형 회귀 (Linear Regression), 로지스틱 회귀 (Logistic Regression), 신경망 (Neural Networks): 이들 알고리즘은 경사 하강법을 사용하여 최적의 파라미터를 찾습니다. 피처 값의 크기가 다르면 경사 하강법의 수렴 속도가 불균형해질 수 있습니다. 스케일링을 통해 학습 속도를 개선하고, 수렴 속도를 균일하게 할 수 있습니다.
✅ 거리 기반 알고리즘 (Distance-based Algorithms)
- K-최근접 이웃 (K-Nearest Neighbors, KNN): 피처 간 거리를 계산하여 가장 가까운 이웃을 찾습니다. 피처 값의 범위가 다르면 특정 피처가 거리 계산에 과도하게 영향을 미칠 수 있습니다. 피처 스케일링을 통해 모든 피처가 동일한 비중으로 거리 계산에 기여하도록 합니다.
- 서포트 벡터 머신 (Support Vector Machine, SVM): SVM은 피처 공간에서의 거리와 각도를 기반으로 최적의 초평면을 찾습니다. 피처 값의 스케일이 다르면 초평면의 위치가 왜곡될 수 있습니다. 스케일링을 통해 정확한 초평면을 찾을 수 있습니다.
✅ 주성분 분석 (Principal Component Analysis, PCA)
PCA는 데이터의 분산을 최대화하는 방향으로 축을 찾습니다. 피처 값의 스케일이 다르면 특정 피처가 분산 계산에 과도하게 기여할 수 있습니다. 스케일링을 통해 모든 피처가 균등하게 분산 계산에 기여하도록 합니다.
✅ 클러스터링 알고리즘 (Clustering Algorithms)
K-평균 (K-Means): 클러스터 중심과 각 데이터 포인트 간의 거리를 기반으로 클러스터를 형성합니다. 피처 값의 스케일이 다르면 특정 피처가 클러스터 형성에 과도하게 영향을 미칠 수 있습니다. 스케일링을 통해 클러스터링의 정확성을 높일 수 있습니다.
데이터의 특성에 따른 필요성
데이터의 특성에 따라 feature scaling이 필요한 경우도 있습니다.
✅ 피처 값의 범위가 크게 다를 때
데이터셋의 피처 값들이 서로 다른 단위를 가지고 있거나, 값의 범위가 매우 다를 때 스케일링이 필요합니다. 예를 들어, 어떤 피처는 0에서 1 사이의 값을 가지는 반면, 다른 피처는 1,000에서 10,000 사이의 값을 가질 수 있습니다. 이러한 경우, 피처 스케일링을 통해 값의 범위를 일치시켜야 합니다.
✅ 이상치(outliers)가 있을 때
데이터셋에 이상치가 포함되어 있을 경우, Min-Max Scaling이나 Standardization을 사용하면 이상치의 영향을 받을 수 있습니다. 이럴 때는 Robust Scaling을 사용하여 중앙값과 IQR을 기준으로 스케일링하는 것이 더 적합할 수 있습니다.
✅ 피처 간의 비중을 동일하게 하고 싶을 때
모든 피처가 모델 학습에 동일한 비중으로 기여하도록 하고 싶을 때 스케일링이 필요합니다. 이는 특정 피처가 모델의 성능에 과도하게 영향을 미치는 것을 방지합니다.
🚨 주요 Feature Scaling 4가지
1️⃣ Min-Max Scaling
Min-Max Scaling은 데이터의 값을 0과 1 사이의 범위로 변환하는 방법입니다. 이 방법은 각 피처의 최소값과 최댓값을 이용하여 데이터를 스케일링합니다.
수학적으로 Min-Max Scaling은 다음과 같이 정의됩니다.
\[ X_{\text{scaled}} = \frac {X - X_{\text {min}}}{X_{\text {max}} - X_{\text {min}}} \]
- \( X \)는 원래의 피처 값입니다
- \( X_{\text{min}} \)는 피처 값의 최솟값입니다
- \( X_{\text {max}} \)는 피처 값의 최댓값입니다
- \( X_{\text {scaled}} \)는 스케일링된 피처 값입니다.
이 방법을 사용하면 모든 피처 값이 0과 1 사이의 값으로 변환됩니다.
🔵 Min-Max Scaling의 장점
- 비교 가능성: 모든 피처 값이 동일한 범위(0-1) 내에 있어 피처 간의 비교가 용이합니다.
🔵 Min-Max Scaling의 단점
- 이상치 민감성: 데이터에 이상치가 있는 경우, 이상치가 스케일링에 큰 영향을 미쳐 다른 데이터 값이 0 또는 1에 가까운 값으로 압축될 수 있습니다.
🔵 Min-Max Scaling의 적용 사례
- 이미지 처리: 픽셀 값(0-255)을 0-1로 변환하여 신경망 모델에 입력합니다.
- 경제 데이터: 주식 가격이나 매출 데이터를 정규화하여 예측 모델에 사용합니다.
- 환경 데이터: 온도, 습도 등의 값을 정규화하여 기후 예측 모델에 적용합니다.
🔵 실습 예제
다음은 Python을 사용하여 Min-Max Scaling을 수행하는 예제입니다. 사이킷런(Scikit-learn) 라이브러리를 사용하여 간단하게 구현할 수 있습니다.
# 필요한 라이브러리 임포트
import numpy as np
from sklearn.preprocessing import MinMaxScaler
# 예제 데이터 생성
data = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12]])
print("원본 데이터:\\\\n", data)
# Min-Max Scaler 객체 생성
scaler = MinMaxScaler()
# 데이터에 Min-Max Scaling 적용
scaled_data = scaler.fit_transform(data)
print("Min-Max Scaling 적용 후 데이터:\\\\n", scaled_data)
===========================================
원본 데이터:
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
Min-Max Scaling 적용 후 데이터:
[[0. 0. 0. ]
[0.33333333 0.33333333 0.33333333]
[0.66666667 0.66666667 0.66666667]
[1. 1. 1. ]]위 코드에서 MinMaxScaler 객체를 생성한 후, fit_transform 메서드를 사용하여 데이터를 스케일링합니다.
이 결과로 모든 피처 값이 0과 1 사이로 변환됩니다.
2️⃣ Standardscaler
Standardscaler은 데이터의 피처 값들을 평균이 0이고 표준편차가 1이 되도록 변환하는 방법입니다. 이는 각 피처 값이 정규 분포(평균이 0, 표준편차가 1)를 따르도록 스케일링하는 것입니다.
수학적으로 Standardization은 다음과 같이 정의됩니다.
\[ X_{\text {scaled}} = \frac{X - \mu}{\sigma} \]
- \( X \)는 원래의 피처 값입니다.
- \( \mu \)는 피처 값의 평균입니다.
- \( \sigma \)는 피처 값의 표준편차입니다.
- \( X_{\text{scaled}} \)는 스케일링된 피처 값입니다.
이 방법을 사용하면 각 피처의 값이 평균 0, 표준편차 1을 가지게 됩니다.
🔵 Standardscaler의 장점
- 정규 분포 데이터 처리: 데이터가 정규 분포를 따를 때 효과적으로 스케일링할 수 있습니다.
- 이상치 완화: 이상치가 있는 경우에도 Min-Max Scaling보다 영향을 덜 받습니다.
- 비교 가능성: 모든 피처가 동일한 스케일을 가지므로 피처 간의 비교가 용이합니다.
🔵 Standardscaler의 단점
- 이해 어려움: Min-Max Scaling에 비해 직관적이지 않으며, 데이터의 상대적인 크기를 파악하기 어렵습니다.
🔵 Standardscaler의 적용사례
- 머신러닝 모델: 로지스틱 회귀, 서포트 벡터 머신(SVM), K-최근접 이웃(KNN) 등 경사 하강법 기반 또는 거리 기반 알고리즘에 사용됩니다.
- 통계 분석: 통계적 가설 검정이나 PCA(주성분 분석)와 같은 분석 방법에서 데이터 정규화에 사용됩니다.
- 신경망: 딥러닝 모델에서 입력 데이터의 분포를 균일하게 하기 위해 사용됩니다.
🔵 실습 예제
다음은 Python을 사용하여 Standardization을 수행하는 예제입니다. 사이킷런(Scikit-learn) 라이브러리를 사용하여 간단하게 구현할 수 있습니다.
# 필요한 라이브러리 임포트
import numpy as np
from sklearn.preprocessing import StandardScaler
# 예제 데이터 생성
data = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12]])
print("원본 데이터:\n", data)
# Standard Scaler 객체 생성
scaler = StandardScaler()
# 데이터에 Standardization 적용
scaled_data = scaler.fit_transform(data)
print("Standardization 적용 후 데이터:\n", scaled_data)
===========================================
원본 데이터:
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
Standardization 적용 후 데이터:
[[-1.34164079 -1.34164079 -1.34164079]
[-0.4472136 -0.4472136 -0.4472136 ]
[ 0.4472136 0.4472136 0.4472136 ]
[ 1.34164079 1.34164079 1.34164079]]위 코드에서 StandardScaler 객체를 생성한 후, fit_transform 메서드를 사용하여 데이터를 스케일링합니다.
이 결과로 모든 피처 값이 평균 0, 표준편차 1로 변환됩니다.
3️⃣ Robust Scaling
Robust Scaling은 중앙값(median)과 사분위 범위(interquartile range, IQR)를 사용하여 데이터를 스케일링하는 방법입니다. 이 방법은 이상치(outliers)의 영향을 최소화하면서 데이터를 스케일링하는 데 유용합니다. Robust Scaler는 중앙값을 0으로, IQR을 1로 맞추어 스케일링합니다.
수학적으로 Robust Scaling은 다음과 같이 정의됩니다.
\[ X_{\text {scaled}} = \frac {X - \text {median}}{\text {IQR}} \]
- \( X \)는 원래의 피처 값입니다.
- \(\text {median}\)은 피처 값의 중앙값입니다.
- \(\text {IQR}\)은 피처 값의 사분위 범위(75번째 백분위수 값 - 25번째 백분위수 값)입니다.
- \( X_{\text {scaled}} \)는 스케일링된 피처 값입니다.
이 방법을 사용하면 데이터의 중앙값이 0이 되고, 사분위 범위가 1이 됩니다.
🔵 Robust Scaling의 장점
- 이상치 민감도 감소: 중앙값과 IQR을 사용하여 스케일링하므로 이상치의 영향을 최소화할 수 있습니다.
- 비교 가능성: 모든 피처가 동일한 스케일을 가지므로 피처 간의 비교가 용이합니다.
- 강건성: 데이터의 분포에 덜 민감하여 비정규 분포 데이터에도 잘 작동합니다.
🔵 Robust Scaling의 단점
- 이해 어려움: Min-Max Scaling에 비해 직관적이지 않으며, 데이터의 상대적인 크기를 파악하기 어렵습니다.
- 계산 복잡성: 중앙값과 IQR을 계산하는 데 시간이 걸릴 수 있습니다.
- 새로운 데이터 처리: 새로운 데이터가 들어올 때, 기존 데이터의 중앙값과 IQR을 사용하여 동일한 방식으로 스케일링해야 합니다.
🔵 Robust Scaling의 적용 사례
- 이상치가 많은 데이터셋: 금융 데이터, 환경 데이터 등 이상치가 많이 포함된 데이터셋에서 유용합니다.
- 머신 러닝 모델: 로지스틱 회귀, 서포트 벡터 머신(SVM), K-최근접 이웃(KNN) 등 경사 하강법 기반 또는 거리 기반 알고리즘에 사용됩니다.
- 의료 데이터: 이상치가 자주 발생하는 의료 데이터에서도 효과적입니다.
🔵 실습 예제
다음은 Python을 사용하여 Robust Scaling을 수행하는 예제입니다. 사이킷런(Scikit-learn) 라이브러리를 사용하여 간단하게 구현할 수 있습니다.
from sklearn.preprocessing import RobustScaler
# 예제 데이터 생성
data = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12],
[100, 200, 300]]) # 이상치 포함
# Robust Scaler 객체 생성
scaler = RobustScaler()
# 데이터에 Robust Scaling 적용
scaled_data = scaler.fit_transform(data)
print("Robust Scaling 적용 후 데이터:\\\\n", scaled_data)
===========================================
Robust Scaling 적용 후 데이터:
[[-1. -1. -1. ]
[-0.5 -0.5 -0.5]
[ 0. 0. 0. ]
[ 0.5 0.5 0.5]
[15.5 32. 48.5]]위 코드에서 RobustScaler 객체를 생성한 후, fit_transform 메서드를 사용하여 데이터를 스케일링합니다.
이 결과로 모든 피처 값이 중앙값을 기준으로 정규화되고, 사분위 범위를 1로 맞추게 됩니다.
4️⃣ MaxAbs Scaling
MaxAbs Scaling은 피처 값들을 각 피처의 절댓값 최댓값으로 나누어 [-1, 1] 범위로 변환하는 방법입니다. 이 방법은 데이터의 스케일을 조정하면서도, 양수와 음수의 비율을 유지합니다.
수학적으로 MaxAbs Scaling은 다음과 같이 정의됩니다.
\[ X_{\text {scaled}} = \frac{X}{|X_{\text {max}}|} \]
- \( X \)는 원래의 피처 값입니다.
- \( |X_{\text{max}}| \)는 피처 값의 절댓값 중 최댓값입니다.
- \( X_{\text {scaled}} \)는 스케일링된 피처 값입니다.
이 방법을 사용하면 데이터의 각 피처 값이 -1과 1 사이로 변환됩니다.
🔵 MaxAbs Scaling의 장점
- 단순성: 계산이 간단하고 직관적입니다.
- 양수와 음수 비율 유지: 데이터의 원래 양수 및 음수 비율을 유지합니다.
- 희소 데이터 처리: 희소 데이터(sparse data)에서도 잘 작동하며, 희소성을 유지합니다.
- 경사 하강법: 경사 하강법 기반 알고리즘의 수렴 속도를 향상합니다.
🔵 MaxAbs Scaling의 단점
- 이상치 민감성: 절댓값 최댓값이 이상치인 경우, 스케일링 결과가 왜곡될 수 있습니다.
- 범위 제한: [-1, 1] 범위로 제한되므로, 특정 상황에서는 다른 스케일링 방법이 더 적합할 수 있습니다.
🔵 MaxAbs Scaling의 적용사례
- 희소 데이터: 텍스트 데이터의 TF-IDF 행렬, 사용자-아이템 행렬 등의 희소 데이터에서 유용합니다.
- 머신러닝 모델: 로지스틱 회귀, 서포트 벡터 머신(SVM), 신경망 등 경사 하강법 기반 알고리즘에 사용됩니다.
- 신호 처리: 신호 데이터의 스케일 조정에 사용됩니다.
🔵 실습 예제
다음은 Python을 사용하여 MaxAbs Scaling을 수행하는 예제입니다. 사이킷런(Scikit-learn) 라이브러리를 사용하여 간단하게 구현할 수 있습니다.
from sklearn.preprocessing import MaxAbsScaler
# 예제 데이터 생성
data = np.array([[1, -2, 3],
[4, 5, -6],
[7, 8, 9],
[-10, 11, -12]])
# MaxAbs Scaler 객체 생성
scaler = MaxAbsScaler()
# 데이터에 MaxAbs Scaling 적용
scaled_data = scaler.fit_transform(data)
print("MaxAbs Scaling 적용 후 데이터:\\\\n", scaled_data)
===========================================
MaxAbs Scaling 적용 후 데이터:
[[ 0.1 -0.18181818 0.25 ]
[ 0.4 0.45454545 -0.5 ]
[ 0.7 0.72727273 0.75 ]
[-1. 1. -1. ]]위 코드에서 MaxAbsScaler 객체를 생성한 후, fit_transform 메서드를 사용하여 데이터를 스케일링합니다. 이 결과로 모든 피처 값이 -1과 1 사이로 변환됩니다.
이와 같이, MaxAbs Scaling은 특히 희소 데이터에서 유용하며, 데이터의 양수 및 음수 비율을 유지하면서 스케일링할 수 있는 방법입니다.
[실습] 데이터셋에서의 Feature Scaling 적용
실습을 위해 간단한 데이터셋을 활용해서 Feature Scaling을 적용해 보도록 하겠습니다.
데이터 출처: Kaggle Diamonds Dataset
데이터셋 소개
해당 데이터셋은 다이아몬드의 가격을 예측하는 데이터셋입니다. 주요 피처는 다음과 같습니다.
- carat: 다이아몬드의 캐럿 무게
- cut: 다이아몬드의 컷 품질 (Fair, Good, Very Good, Premium, Ideal)
- color: 다이아몬드의 색상 (D ~ J)
- clarity: 다이아몬드의 투명도 (I1, SI2, SI1, VS1, VS2, VVS1, VVS2, IF)
- depth: 전체 깊이 퍼센트 = z / mean(x, y)
- table: 다이아몬드의 상단 폭의 비율
- price: 다이아몬드의 가격 (USD)
- x: 길이 (mm)
- y: 폭 (mm)
- z: 깊이 (mm)
아래 데이터셋에서 carat, depth, table, price, x, y, z 칼럼은 수치형(numerical) 데이터로 구성되어 있지만, 이들은 서로 다른 범위(scale)를 가지고 있습니다. 따라서, carat, depth, table, price, x, y, z 칼럼에 대해서 표준화(Standardization)를 적용할 예정입니다.
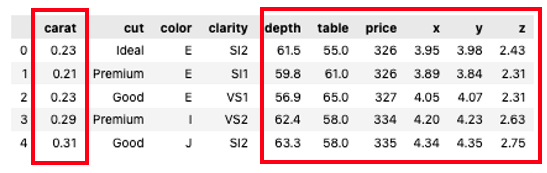
데이터 로드
우선 데이터를 로드하고, 필요한 피처를 선택하여 전처리를 진행하도록 하겠습니다.
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
data = pd.read_csv('diamonds.csv', encoding='cp949')
data.head()

종속 변수와(X) 독립 변수(y) 설정
간단한 실험을 위해 수치형 피처만 추출한 뒤 종속 변수와 독립 변수를 지정해 주도록 하겠습니다.
만약, 범주형 변수도 넣고 싶다면. 수치형 변수로 변경을 해준 뒤 넣으면 되겠죠!?
(가격을 예측해야 하므로 'price'를 y로 설정)
X = data[['carat', 'depth', 'table', 'price', 'x', 'y','z']]
y = data['price']
# train, valid 분리
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.2, random_state=42)자, 이제 우리가 모델을 학습하고 예측하는데 필요한 피처를 모두 선택했습니다.
feature Scailing 적용 x
우선 feature scailing을 적용하지 않고 성능이 어느 정도 나오는지 확인을 해보겠습니다.
model = LinearRegression()
model.fit(X_train, y_train)
y_pred_baseline = model.predict(X_valid)
baseline_rmse = np.sqrt(mean_squared_error(y_valid, y_pred_baseline))
print(f"Baseline RMSE: {baseline_rmse}")
> Baseline RMSE: 3.2910446545463946e-12RMSE: 3.2910446545463946 e-12는 예측 모델이 매우 높은 정확도로 예측을 하고 있다는 것을 의미합니다. RMSE (Root Mean Squared Error)는 예측 값과 실제 값 간의 차이를 측정한 것이며, 값이 작을수록 모델의 예측이 정확하다는 것을 나타냅니다.
이제는 다양한 스케일링 방법을 적용하고 예측 모델을 학습 및 평가해 보겠습니다.
1️⃣ MinMaxScaler 적용 O
* 참고 : train 데이터셋에서 특정 feature(carat, depth, table, price, x, y, z)에 대해서 feature scaling를 적용하였다면, test, valid 데이터셋에도 동일한 feature(carat, depth, table, price, x, y, z )에 대해서 feature scaling을 적용해야 합니다.
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
model_scaled = LinearRegression()
model_scaled.fit(X_train_scaled, y_train)
y_pred_scaled = model_scaled.predict(X_valid_scaled)
MinMax_rmse = np.sqrt(mean_squared_error(y_valid, y_pred_scaled))
print(f"MinMaxScaler RMSE: {MinMax_rmse}")
> MinMaxScaler RMSE: 1.8670146374176256e-12
RMSE 값은 작을수록 모델의 예측 성능이 더 좋다는 것을 의미합니다. 두 값 중 1.8670146374176256 e-12가 3.2910446545463946 e-12보다 작기 때문에, MinMaxScaler를 적용한 경우가 더 좋은 성능을 보였습니다.
MinMaxScaler 변환 확인
MinMaxScaler를 적용함으로써 데이터셋이 0과 1 사이의 값들로 변경이 잘 되었는지 확인해 보겠습니다.
X_train_scaled
> array([[0.37629938, 0.41944444, 0.40384615, ..., 0.76629423, 0.13904924,
0.15 ],
[0.16839917, 0.47222222, 0.32692308, ..., 0.61173184, 0.11018676,
0.12327044],
[0.18711019, 0.54166667, 0.28846154, ..., 0.61359404, 0.11103565,
0.12893082],
...,
[0.02702703, 0.48055556, 0.28846154, ..., 0.41806331, 0.07572156,
0.08490566],
[0.14553015, 0.55 , 0.30769231, ..., 0.5707635 , 0.10237691,
0.12012579],
[0.1954262 , 0.48333333, 0.28846154, ..., 0.63500931, 0.11528014,
0.12924528]])
# MinMaxScaler 적용 후 데이터셋이 0~1 사이에 있는지 확인
print("X_train_scaled 범위:")
print(f"최소값: {X_train_scaled.min(axis=0)}")
print(f"최대값: {X_train_scaled.max(axis=0)}")
> X_train_scaled 범위:
> 최소값: [0. 0. 0. 0. 0. 0. 0.]
> 최대값: [1. 1. 1. 1. 1. 1. 1.]
2️⃣ StandardScaler 적용 O
from sklearn.preprocessing import StandardScaler
# StandardScaler 적용 후 예측
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
model_scaled = LinearRegression()
model_scaled.fit(X_train_scaled, y_train)
y_pred_scaled = model_scaled.predict(X_valid_scaled)
Standard_rmse = np.sqrt(mean_squared_error(y_valid, y_pred_scaled))
print(f"StandardScaler RMSE: {Standard_rmse}")
> StandardScaler RMSE: 2.33335419941004e-12StandardScaler를 적용하지 않은 성능보다 성능이 향상되었습니다.
StandardScaler 변환 확인
print("X_train_scaled 범위:")
print(f"평균: {X_train_scaled.mean(axis=0)}")
print(f"표준편차: {X_train_scaled.std(axis=0)}")
X_train_scaled 범위:
평균: [-4.84101697e-17 2.57932348e-15 1.49478748e-15 1.81126485e-18
1.15484600e-15 -3.13101829e-16 -1.12862383e-15]
표준편차: [1. 1. 1. 1. 1. 1. 1.]
평균
각 피처의 평균값이 거의 0에 가깝습니다. 이는 StandardScaler가 각 피처를 평균 0으로 맞추어 변환했음을 의미합니다. 숫자들이 매우 작은 값(거의 0에 가까움)인 이유는 컴퓨터의 부동 소수점 연산의 특성으로 인한 것입니다.
표준편차
각 피처의 표준편차가 1입니다. 이는 StandardScaler가 각 피처의 값을 변환하여 분산이 1이 되도록 조정했음을 의미합니다. 결과적으로 모든 피처가 동일한 스케일(평균 0, 표준편차 1)을 가지게 됩니다.
3️⃣ RobustScaler 적용 O
from sklearn.preprocessing import RobustScaler
# RobustScaler 적용 후 예측
scaler = RobustScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
model_scaled = LinearRegression()
model_scaled.fit(X_train_scaled, y_train)
y_pred_scaled = model_scaled.predict(X_valid_scaled)
Robust_rmse = np.sqrt(mean_squared_error(y_valid, y_pred_scaled))
print(f"RobustScaler RMSE: {Robust_rmse}")
> RobustScaler RMSE: 2.1643330814000257e-12RobustScaler를 적용하지 않은 성능보다 성능이 향상되었습니다.
RobustScaler 변환 확인
# 중앙값과 사분위 범위 출력
def calculate_iqr(data):
return np.percentile(data, 75, axis=0) - np.percentile(data, 25, axis=0)
print("스케일된 데이터의 중앙값:\\n", np.median(X_train_scaled, axis=0))
print("스케일된 데이터의 사분위 범위 (IQR):\\n", calculate_iqr(X_train_scaled))
> 스케일된 데이터의 중앙값: [0. 0. 0. 0. 0. 0. 0.]
> 스케일된 데이터의 사분위 범위 (IQR): [1. 1. 1. 1. 1. 1. 1.]중앙값을 0으로, IQR을 1로 변환이 된 것을 확인할 수 있습니다.
4️⃣ MaxAbsScaler 적용 O
from sklearn.preprocessing import MaxAbsScaler
# MaxAbsScaler 적용 후 예측
scaler = MaxAbsScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
model_scaled = LinearRegression()
model_scaled.fit(X_train_scaled, y_train)
y_pred_scaled = model_scaled.predict(X_valid_scaled)
MaxAbs_rmse = np.sqrt(mean_squared_error(y_valid, y_pred_scaled))
print(f"MaxAbsScaler RMSE: {MaxAbs_rmse}")
> MaxAbsScaler RMSE: 1.4230549736653272e-12MaxAbsScaler를 적용하지 않은 성능보다 성능이 향상되었습니다. 가장 향상이 많이 되었네요!
MaxAbsScaler 변환 확인
# MaxAbsScaler 적용 후 데이터의 최대값과 최소값 확인
print("MaxAbsScaler 적용 후 X_train_scaled 범위:")
print(f"최소값: {X_train_scaled.min(axis=0)}")
print(f"최대값: {X_train_scaled.max(axis=0)}")
MaxAbsScaler 적용 후 X_train_scaled 범위:
최소값: [0.03992016 0.5443038 0.45263158 0.01732384 0. 0.
0. ]
최대값: [1. 1. 1. 1. 1. 1. 1.]피처 값이 -1과 1 사이로 변환된 것을 확인할 수 있습니다.
결론
| RMSE | |
| feature Scaling X | 3.2910446545463946e-12 |
| MinMaxScaler | 1.8670146374176256e-12 |
| StandardScaler | 2.33335419941004e-12 |
| RobustScaler | 2.1643330814000257e-12 |
| MaxAbsScaler | 1.4230549736653272e-12 |
위 결과를 바탕으로 다음과 같은 결론을 내릴 수 있습니다.
- 가장 효과적인 스케일링 방법: MaxAbsScaler
- 모든 스케일링 방법 중 RMSE 값이 가장 낮아, 모델의 예측 성능을 가장 크게 개선했습니다.
- 비교적 효과적인 스케일링 방법: MinMaxScaler, RobustScaler
- 이 두 방법도 Feature Scaling을 적용하지 않은 경우보다 성능을 개선하는 데 도움이 되었습니다.
- 덜 효과적인 스케일링 방법: StandardScaler
- 다른 방법들에 비해 성능 개선이 상대적으로 적었습니다.
👉 전반적으로 Feature Scaling을 적용하는 것이 모델의 성능을 개선하는 데 도움이 되었음을 확인할 수 있습니다. 특히, MaxAbsScaler가 가장 큰 개선을 보였습니다.
🚨 추가 고려 사항 (모든 데이터에 대해서 항상 위와 같은 결과가 나오는 것은 아님!)
- 데이터 특성: 데이터의 특성에 따라 어떤 스케일링 방법이 가장 효과적인지 달라질 수 있습니다. 따라서 항상 동일한 결과를 보장하지는 않으며, 데이터셋에 따라 최적의 스케일링 방법을 선택해야 합니다.
- 모델의 일반화 성능: RMSE 값이 매우 작기 때문에, 모델이 데이터에 과적합(overfitting)되었을 가능성을 염두에 두고 새로운 데이터에서도 성능이 유지되는지 확인하는 것이 중요합니다.
[Data leakage 주의]
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
만약 위와 같이 코드를 작성할 경우 test 데이터셋의 평균과 표준편차의 값들을 계산하고, 계산된 평균과 표준편차를 이용해서 표준화를 진행하게 됩니다. 하지만 이런 경우는 test 데이터셋의 통계치를 사용하므로 data leakage에 해당합니다. test 데이터셋은 미래의 데이터이기 때문에 미래의 데이터를 이용하는 것은 불가능합니다.
그러므로 test 데이터셋에 대해서는 fit() 메서드를 사용하지 않고, train 데이터셋에서 계산된 평균과 표준편차 등의 값을 그대로 이용하여 표준화를 진행해야 합니다.
# 중요!!!! 학습/테스트 데이터의 스케일링 변환 시 유의점
학습 데이터로 fit(), transform()을 적용한 후 테스트 데이터에서는 다시 fit()을 수행하지 않고 학습 데이터로 fit()을 적용한 결과를 이용해서 transform()을 적용해야 한다.
학습 데이터로 fit() -> 학습 데이터로 transform() => 테스트 데이터로 transform()
옮은 코드
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
train[features] = scaler.fit_transform(train[features]) # fit_transform
test[features] = scaler.transform(test[features]) # transform옮지 않은 코드
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
train[features] = scaler.fit_transform(train[features]) # fit_transform
test[features] = scaler.fit_transform(test[features]) # fit_transform
'pythonML' 카테고리의 다른 글
| [pythonML] 결정 트리 (Decision Tree) (0) | 2022.03.20 |
|---|---|
| [pythonML] 머신러닝으로 타이타닉 생존자 예측 (0) | 2022.03.19 |
| [pythonML] 레이블 인코딩(label encoding) / 원-핫 인코딩(one hot encoding)- 데이터 전처리 (0) | 2022.03.04 |
| [pythonML] cross_val_score(교차검증)/ GridSearchCV(교차검증, 최적 하이퍼 파라미터 튜닝) (0) | 2022.03.02 |
| [pythonML] K-fold / stratifiedKFold - 교차검증 (0) | 2022.03.02 |