분류는 2개의 결괏값만 가지는 이진분류와,
여러 개의 결괏값을 가지는 다중 분류로 나뉠 수 있다.
- 정밀도
- 재현율
- F1 score
- ROC AUC
이 네 가지 지표는 다중분류보다 이중 분류에서 중요하게 강조하는 지표이다.
1. 정확도 (Accuracy)
정확도는 실제 데이터에서 예측 데이터가 얼마나 같은지를 판단하는 지표이다.
하지만 이진 분류의 경우 데이터의 구성에 따라 모델의 성능을 왜곡할 수 있기 때문에 정확도 수치 하나만 가지고 성능을 평가하지는 않는다.
ex) 타이타닉 탑승객이 여자인 경우에 생존 확률이 높은 경우 (여 90 남 10)
무조건 성별이 여자는 생존, 남자는 사망으로 예측해도 정확도가 높은 수치가 나올 수 있다.
→ 즉, 정확도는 불균형한(Imbalanced) 레이블 값 분포에서는 적합한 평가 지표가 아니다.
2. 오차 행렬 (Confusion matrix)
학습된 분류 모델이 예측을 수행하면서 얼마나 헷갈리고 있는지도 보여주는 지표이다.
이진 분류의 예측 오류가 얼마인지 & 어떠한 유형의 예측 오류가 발생하고 있는지
3. 정밀도(precision)와 재현율(recall)
정밀도와 재현율은 Positive 데이터 세트의 예측 성능에 초점을 맞춘 평가 지표이다.
** 일반적으로 불균형한 레이블 클래스를 가지는 이진 분류 모델에서는
찾아야 하는 매우 적은 수의 결괏값을 1로, 그렇지 않은 경우 0으로 부여하는 경우가 많다.
→ 즉, Negaive 가 Positive 보다 많다.
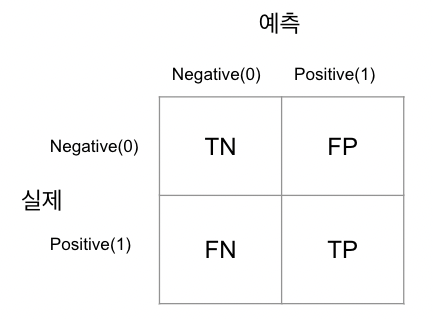
- 정확도 = ( TN + TP )/( TN + TP + FP + FN )
- 정밀도 = TP / (FP + TP)
- 재현율 = TP / (FN + TP)
정밀도 (precision) : 예측을 Positive 로 한 대상 중 예측과 실제 값이 Positive로 일치한 데이터의 비율 (Positive 예측 성능을 더욱 정밀하게 측정하기 위한 평가 지표)
재현율 & 민감도(recall & sensitivity) : 실제 값이 Positive인 대상 중 예측과 실제 값이 Positive 로 일치한 데이터의 비율
정밀도와 재현율 지표 중에 이진 분류 모델의 업무 특성에 따라서 특정 평가 지표가 더 중요한 지표로 간주될 수 있다.
재현율이 중요한 경우는 실제 Positive 양성 데이터를 Negative 로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우이다.
- 암 판단 모델 - 실제 Positive 인 암 환자를 Negative 음성으로 잘못 판단했을 경우 생명을 앗아갈 정도로 심각하기 때문이다. 반면 건강한 환자를 암 환자로 예측한 경우면 다시 한번 재검사를 하는 수준의 비용이 소모될 것이다.
- 보험 사기 & 금융 사기 적발 - 금융거래 사기인 Positive 를 Negative로 잘못 판단하게 되면 회사에 미치는 손해가 클 것. 반면 정상 금융거래를 금융사기로 잘못 판단하더라도 다시 한번 금융사기인지 재확인하는 절차를 가지면 된다.
정밀도가 중요한 경우는 실제 Negative 음성 데이터를 Positive 로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우이다.
- 스팸 메일 여부 판단 - 실제 Positive 인 스팸 메일을 Negative 인 일반 메일로 분류하더라도 사용자가 불편함을 느끼는 정도이지만, 실제 Negative 인 일반 메일을 Positive 인 스팸 메일로 분류할 경우에는 메일을 아예 받지 못하게 돼 업무에 차질이 생긴다.
재현율과 정밀도 모두 TP 를 높이는 데 동일하게 초점을 맞추지만, 재현율은 FN를 낮추는데, 정밀도는 FP를 낮추는 데 초점을 맞춘다.
이 같은 특성 때문에 재현율과 정밀도는 서로 보완적인 지표로 분류의 성능을 평가하는 데 적용된다. 가장 좋은 성능평가는 재현율과 정밀도 모두 높은 수치를 얻는 것. (반면 둘 중 어느 한 평가 지표만 매우 높고, 다른 수치는 매우 낮은 결과를 나타내는 경우엔 바람직하지 않다)
4. F1 score
F1 score 는 정밀도와 재현율을 결합한 지표입니다.
정밀도와 재현율이 어느 한쪽으로 치우치지 않는 수치를 나타낼 때 상대적으로 높은 값을 가집니다.

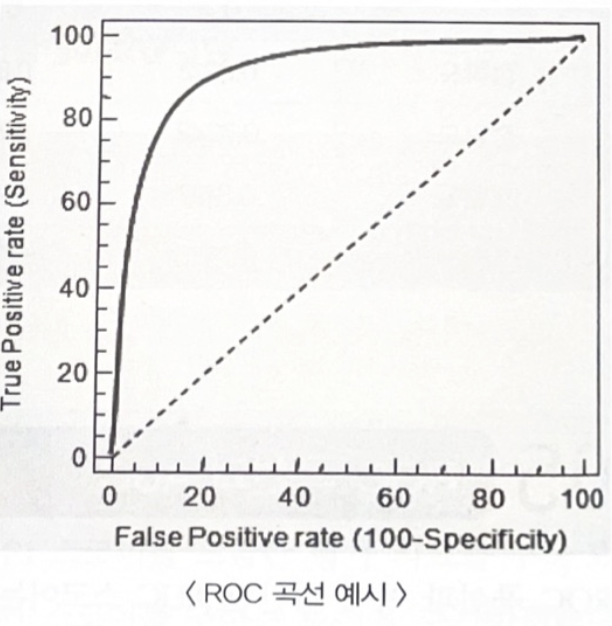
5. ROC 곡선과 AUC
ROC 곡선과 AUC 스코어는 이진 분류의 예측 성능 측정에서 중요하게 사용되는 지표입니다.
ROC 곡선 : FPR 가 변할 때 TPR 이 어떻게 변하는지를 나타내는 곡선 (FPR : X축 , TPR : Y축)
TPR(재현율 = 민감도) = TP / (FN + TP)
TNR(특이성) = TN / (TN + FP)
FPR = 1 - TNR (특이성)
ROC 곡선이 직선에 가까울수록 성능이 떨어지는 것이며, 멀어질수록 성능이 뛰어난 것이다. 임계값을 변화시키며 FPR을 0부터 1까지 변경하면서 TPR의 변화를 구한다.
AUC : 가능한 모든 임곗값에서 집계된 성능 측정값을 제공한다. AUC값은 ROC 곡선 밑의 면적을 구한 것이며 1에 가까울수록 좋은 수치이다.
FPR이 작은 상태에서 얼마나 큰 TPR을 얻을 수 있는지를 찾는 것.
임계값을 낮추면 더 많은 양성 값을 얻게 되므로 민감도(sensitivity)는 증가, 특이도(specificity)는 감소
임계값을 높이면 더 많은 음성 값을 얻게 되므로 특이도(Specificity)는 증가, 민감도(sensitivity)는 감소
'pythonML' 카테고리의 다른 글
| [pythonML] XGBoost 하이퍼파라미터 (0) | 2023.06.13 |
|---|---|
| [pythonML] 랜덤포레스트(RandomForest) 하이퍼파라미터(RandomForestClassifier, RandomForestRegressor) (0) | 2023.06.09 |
| [pythonML] 회귀 트리 (0) | 2022.07.16 |
| [pythonML] 회귀- 다항회귀 (0) | 2022.07.16 |
| [pythonML] 부스팅(Boosting)-LGBM(Light Gradient Boost Machine) (0) | 2022.07.15 |