DNN과 RNN 비교
딥러닝에서 데이터의 시간적 연속성을 처리하는 방법은 모델 선택에 중요한 영향을 미치는데요. 우선 DNN과 RNN을 비교하여 시간적 연속성의 중요성을 살펴보시죠.
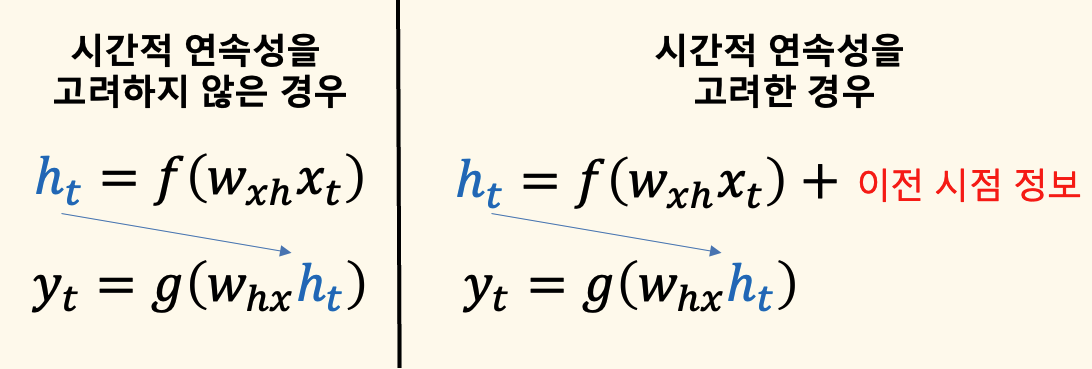
시간적 연속성을 고려하지 않은 경우
- 왼쪽의 수식에서는 입력 데이터 \( x_t \)가 주어졌을 때, 은닉층 \( h_t \)가 가중치 \( W_{xh} \)와 활성화 함수 \( f(\cdot) \)을 통해 계산됩니다. 이 은닉층의 출력 \( h_t \)는 다시 가중치 \( W_{hx} \)와 활성화 함수 \( g(\cdot) \)를 거쳐 최종 출력값 \( y_t \)를 생성합니다.
- 이 경우, 각 시점 \( t \)의 데이터는 독립적으로 처리됩니다. 이전 시점의 정보는 고려되지 않으므로, 모델은 시간적 연속성이나 데이터 간의 상관관계를 학습할 수 없습니다. 이는 일반적인 DNN이 사용하는 방식입니다.
시간적 연속성을 고려한 경우
- 오른쪽의 수식에서는 입력 데이터 \( x_t \)가 주어졌을 때, 은닉층 \( h_t \)를 계산할 때 이전 시점의 정보가 추가로 고려됩니다. 수식에서 볼 수 있듯이, \( h_t \)는 가중치 \( W_{xh} \)와 \( x_t \)뿐만 아니라, 이전 시점의 은닉층 출력(이전 시점 정보)도 함께 고려됩니다.
- 이 방식은 RNN(Recurrent Neural Network)의 기본 원리로, 시간적 순서와 연속성을 반영하여 데이터를 처리합니다. 이렇게 하면, 모델이 과거의 정보를 바탕으로 현재의 출력을 예측할 수 있게 됩니다. 따라서, 시계열 데이터나 자연어 처리와 같은 연속된 데이터에서 사용하면 좋겠죠.
이전 시점 정보를 어떻게 반영할까?
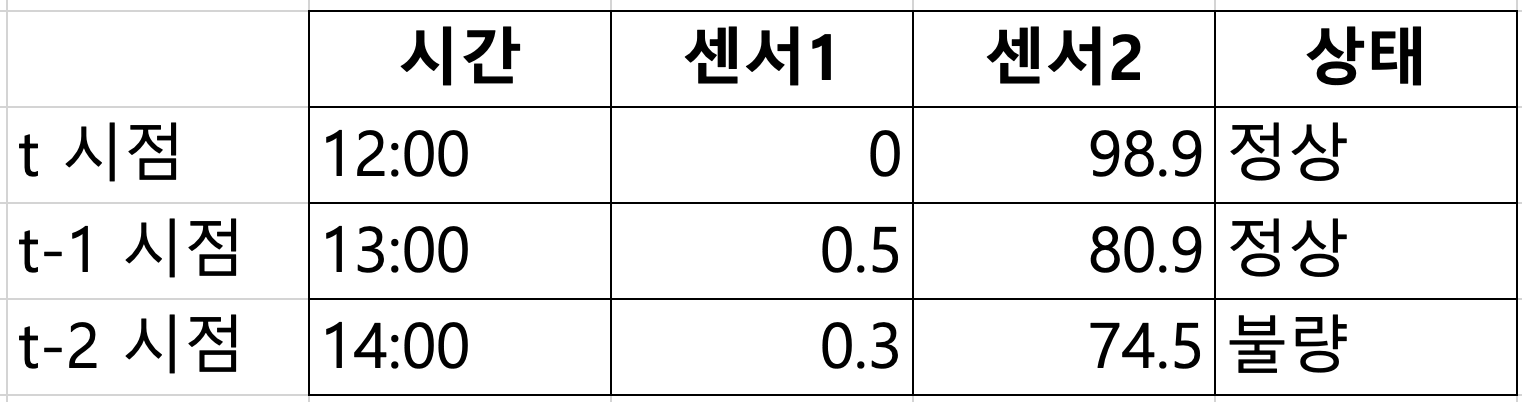
우리가 예시로 사용할 데이터셋은 시간에 따른 센서 값의 변화를 기록한 시계열 데이터입니다. 데이터셋은 세 개의 시점에서 수집된 값들을 포함하고 있으며, 각 시점은 '시간', '센서 1', '센서 2', '상태'라는 네 가지 변수로 구성되어 있습니다.
- 시간: 데이터가 기록된 시점을 나타내며, 각 시점은 t, t-1, t-2로 표현됩니다.
- 센서1: 첫 번째 센서에서 수집된 값을 나타냅니다. 이 값은 시점에 따라 변화하며, 각 시점의 상태를 예측하는 데 중요한 역할을 합니다.
- 센서2: 두 번째 센서에서 수집된 값으로, 이 역시 상태 예측에 중요한 변수를 제공합니다.
- 상태: 각 시점에서 기록된 시스템의 상태를 나타내며, '정상' 또는 '불량'으로 표시됩니다.
이 데이터셋을 통해 우리는 시간에 따라 변화하는 센서 값이 시스템의 상태에 어떻게 영향을 미치는지를 분석할 수 있습니다. 또한, RNN 모델이 어떻게 이전 시점의 정보를 활용하여 현재 시점의 상태를 예측하는지를 이해할 수 있게 됩니다.
시간적 연속성을 고려하지 않은 경우
우선 시간적 연속성을 고려하지 않은 경우, DNN(Deep Neural Network) 모델이 어떻게 동작하는지를 시각적으로 보시죠.
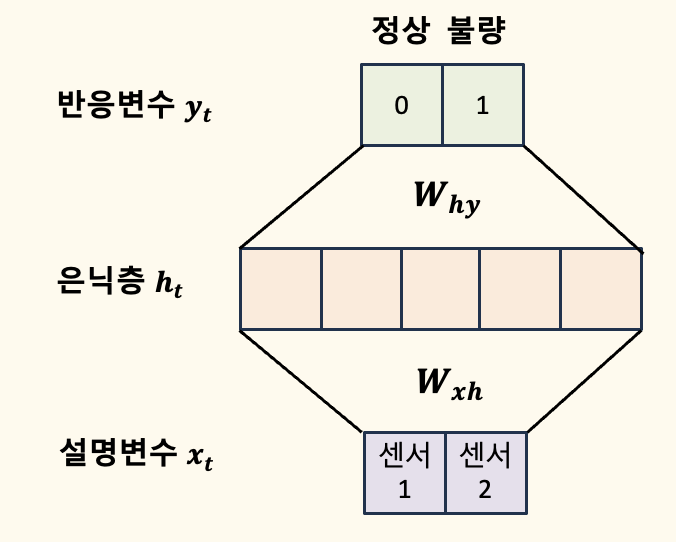
설명 변수 \( x_t \)는 센서 1과 센서 2에서 수집된 데이터로 구성됩니다. 이 입력 데이터는 은닉층 \( h_t \)로 전달되어, 가중치 \( W_{xh} \)와 결합됩니다. 은닉층은 입력 데이터를 바탕으로 중요한 특징을 추출하는 역할을 하며, 이 특징은 다음 단계에서 반응 변수 \( y_t \)를 예측하는 데 사용됩니다.
예측된 반응 변수 \( y_t \)는 출력층에서 계산되며, 가중치 \( W_{hy} \)와 은닉층의 출력 \( h_t \)을 결합하여 결정됩니다. 이 모델에서는 '정상'과 '불량'이라는 두 가지 상태 중 하나를 예측합니다.
이 모델의 중요한 특징은 각 시점의 데이터를 독립적으로 처리한다는 점입니다. 즉, 현재 시점의 센서 데이터만을 바탕으로 상태를 예측하며, 이전 시점의 정보는 반영되지 않습니다. 이러한 접근 방식은 시계열 데이터에서의 시간적 상관관계를 고려하지 않는 일반적인 DNN의 방식입니다.
시간적 연속성을 고려한 경우 (t-1까지 고려)
시간적 연속성을 고려한 RNN(Recurrent Neural Network) 모델이 어떻게 동작하는지를 설명하고 있습니다. 특히, 현재 시점 \( t \)의 예측을 위해 이전 시점 \( t-1 \)의 정보를 어떻게 활용하는지를 보여줍니다.

위쪽의 이미지는 은닉층에 이전 시점의 은닉층 출력을 추가하는 과정을 나타냅니다. 시간적 연속성을 고려하지 않은 모델과 비교했을 때, 이 방식에서는 이전 시점의 은닉층 출력 \( h_{t-1} \)이 현재 시점의 은닉층 출력 \( h_t \)를 계산할 때 사용됩니다. 이 과정을 통해 모델은 이전 시점의 정보를 고려하여 현재 시점의 출력을 더 정확하게 예측할 수 있죠.
아래쪽의 이미지는 RNN 모델의 전체 구조를 보여줍니다. 이 구조에서는 두 가지 중요한 입력이 있습니다.
1. 현재 시점의 설명 변수 \( x_t \) (센서 1, 센서 2 값)
2. 이전 시점의 은닉층 출력 \( h_{t-1} \)
이 두 입력은 각각 가중치 \( W_{xh} \)와 \( W_{hh} \)를 통해 은닉층 \( h_t \)로 전달됩니다. 여기서 \( W_{xh} \)는 현재 시점의 설명 변수를 처리하는 가중치이고, \( W_{hh} \)는 이전 시점의 은닉층 출력을 처리하는 가중치입니다. 두 가중치의 결과가 합쳐져 은닉층 \( h_t \)가 계산됩니다.
이렇게 계산된 은닉층 \( h_t \)는 다시 가중치 \( W_{hy} \)를 거쳐 최종 출력 \( y_t \)를 생성합니다.
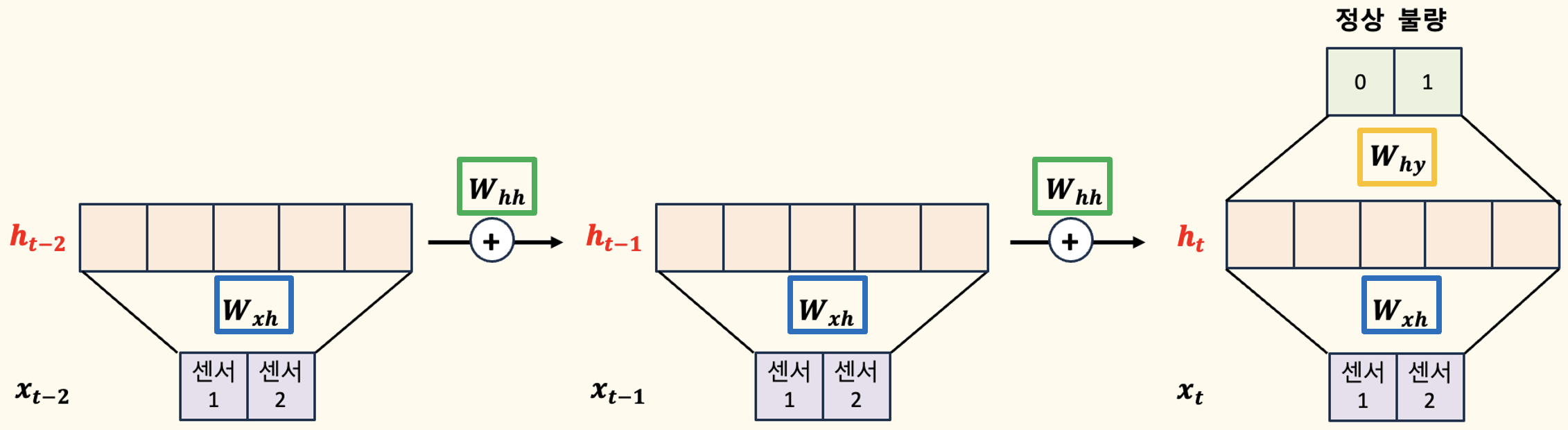
시간적 연속성을 고려한 경우 (t-2까지 고려)
RNN 모델이 현재 시점 \( t \)의 출력을 예측하기 위해 \( t-1 \) 시점뿐만 아니라 \( t-2 \) 시점까지의 정보가 어떻게 활용되는지를 살펴봅시다.
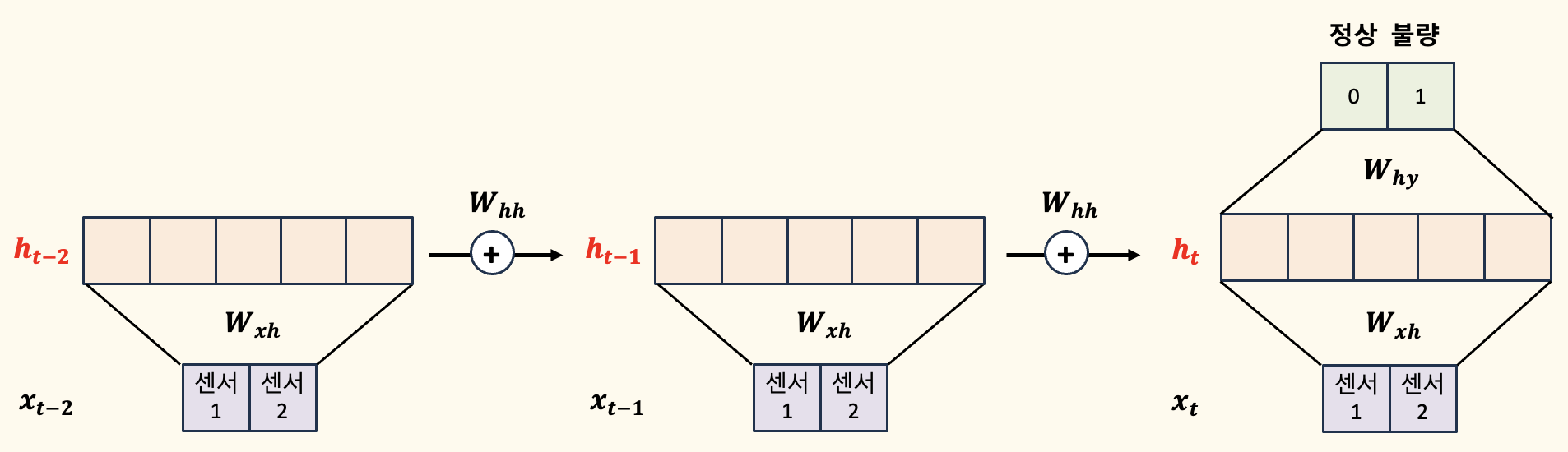
각 시점의 은닉층 출력이 다음 시점의 은닉층 입력에 포함되는 과정을 단계별로 나타내고 있습니다.
- 첫 번째 단계 (시점 \( t-2 \)):
- 입력 변수 \( x_{t-2} \)가 은닉층 \( h_{t-2} \)로 전달됩니다.
- 은닉층 \( h_{t-2} \)의 출력은 가중치 \( W_{hh} \)를 통해 다음 시점인 \( t-1 \) 시점으로 전달됩니다.
- 두 번째 단계 (시점 \( t-1 \)):
- \( t-1 \) 시점에서의 입력 변수 \( x_{t-1} \)가 은닉층 \( h_{t-1} \)로 전달되며, 동시에 이전 시점 \( h_{t-2} \)의 출력이 함께 고려됩니다.
- 이 과정에서 이전 시점의 정보가 가중치 \( W_{hh} \)를 통해 은닉층 \( h_{t-1} \)로 전달됩니다.
- 세 번째 단계 (시점 \( t \)):
- 현재 시점 \( t \)에서의 입력 변수 \( x_t \)가 은닉층 \( h_t \)로 전달되고, 동시에 이전 시점 \( h_{t-1} \)의 출력이 함께 고려됩니다.
- 이 정보들은 결합되어 가중치 \( W_{hy} \)를 통해 최종 출력 \( y_t \)를 생성합니다.
위 과정을 수식으로 나타냅니다.
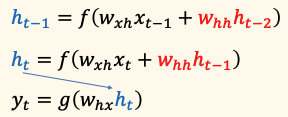
- 은닉층 \( h_{t-1} \)는 \( t-1 \) 시점의 입력 \( x_{t-1} \)와 함께 \( t-2 \) 시점의 은닉층 출력 \( h_{t-2} \)를 고려하여 계산됩니다.
- 마찬가지로 은닉층 \( h_t \)는 \( t \) 시점의 입력 \( x_t \)와 \( t-1 \) 시점의 은닉층 출력 \( h_{t-1} \)를 바탕으로 계산됩니다.
- 최종 출력 \( y_t \)는 이 은닉층 \( h_t \)를 기반으로 계산됩니다.
이 과정은 RNN이 과거 여러 시점에 걸친 정보를 누적적으로 반영하여 예측을 수행할 수 있음을 보여줍니다. 특히, 시간적 연속성이 중요한 데이터에서는 이러한 방법이 매우 유용하며, 과거 정보가 반영될수록 더 정확한 예측을 할 수 있습니다.
RNN의 파라미터 3가지
1. 입력 가중치 \( W_{xh} \)
- 입력 데이터 \( x_t \)에서 은닉층 \( h_t \)로 연결되는 가중치입니다. RNN이 입력 데이터를 은닉 상태로 변환하는 데 사용됩니다. 각 입력 특성에 대해 은닉층 뉴런에 얼마나 영향을 미치는지를 결정합니다.
2. 은닉층 가중치 \( W_{hh} \)
- 이전 시점의 은닉 상태 \( h_{t-1} \)에서 현재 시점의 은닉 상태 \( h_t \)로 연결되는 가중치입니다. RNN의 핵심적인 특성인 순환(recurrent) 구조를 가능하게 하며, 과거 정보를 현재 예측에 반영할 수 있도록 합니다.
3. 출력 가중치 \( W_{hy} \)
- 은닉층 \( h_t \)에서 출력 \( y_t \)로 연결되는 가중치입니다. 은닉 상태에서 최종 출력으로 변환하는 데 사용되며, 예측된 값을 계산하는 역할을 합니다. 이 가중치는 RNN이 학습한 은닉 상태를 바탕으로 최종 출력을 생성합니다.
RNN의 가중치와 반복 구조
RNN에서 출력 가중치 \( W_{hy} \)는 은닉층 \( h_t \)에서 출력층으로 전달되는 유일한 가중치로, 모델의 학습 과정에서 은닉 상태가 학습한 패턴을 바탕으로 최종 출력을 생성합니다. 따라서, 이 가중치는 각 시점 \( t \)에서 딱 한 번만 사용됩니다.
반면에, 입력 가중치 \( W_{xh} \)와 은닉층 가중치 \( W_{hh} \)는 여러 시점에 걸쳐 반복적으로 사용됩니다.
입력 가중치 \( W_{xh} \)는 각 시점에서 입력 \( x_t \)를 은닉 상태 \( h_t \)로 변환하는 데 사용됩니다. 모든 시점에서 동일한 가중치가 사용되며, 각 시점에서 입력 데이터가 은닉 상태로 변환될 때마다 반복적으로 적용되죠.
은닉층 가중치 \( W_{hh} \)도 마찬가지로, 이전 시점의 은닉 상태 \( h_{t-1} \)를 현재 시점의 은닉 상태 \( h_t \)로 변환하는 데 사용됩니다. 이 가중치도 모든 시점에서 동일하게 사용되며, 시점 간의 정보를 전달하고 연속성을 유지합니다.
이러한 특징들 때문에, 이 두 가지 가중치는 여러 시점에 걸쳐 동일하게 적용되며, 아래와 같은 그림으로 하나의 이미지로 표현할 수 있습니다.

즉, RNN 모델은 이전 시점의 모든 정보를 활용하여 현재 시점의 y를 예측합니다. 이 과정에서 사용되는 모든 파라미터는 시점 간에 공유됩니다.
RNN 구조의 종류
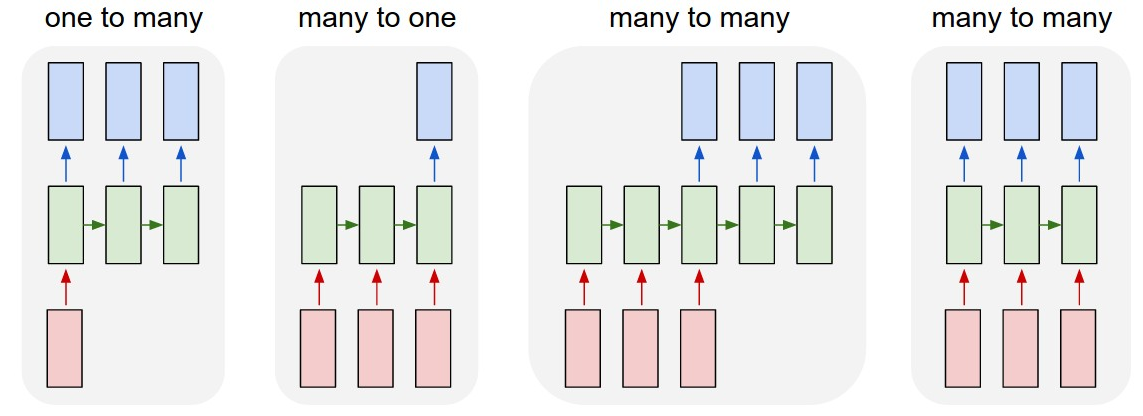
1. One-to-Many 구조 - 이미지 캡셔닝
하나의 입력이 여러 출력 시퀀스로 연결되는 구조입니다. 예를 들어, 이미지에서 캡션을 생성하는 작업에 사용됩니다. 이미지를 하나의 입력으로 받아 RNN이 연속적인 텍스트(예: "고양이가 소파에 앉아 있다")를 출력하는 구조입니다.
2. Many-to-One 구조 - 긍정/부정
여러 입력 시퀀스가 주어졌을 때 하나의 출력으로 연결되는 구조입니다. 예를 들어, 텍스트의 여러 단어를 입력으로 받아, 문장의 감정(긍정/부정)과 같은 하나의 출력을 생성하는 감정 분석 작업에 많이 사용됩니다.
3.Many-to-Many 구조 (Many-to-One + One-to-Many) - 번역
입력 시퀀스와 출력 시퀀스가 다른 길이를 가질 수 있는 구조입니다. 대표적인 예로, 기계 번역과 같은 시퀀스 변환 작업을 들 수 있습니다.
예를 들어, 영어 문장이 입력으로 주어지고, 대응하는 한글 문장이 출력으로 생성되는 과정입니다. “How are you? “라는 영어 문장이 입력으로 주어지면, RNN 인코더가 이 문장을 처리하여 하나의 요약된 은닉 상태로 압축합니다. 이후에, 디코더는 “어떻게” -> “지내” -> “세요? “와 같이 순차적으로 한글 문장을 생성합니다. 이 과정에서 입력과 출력 시퀀스의 길이는 다를 수 있습니다.
4. Many-to-Many 구조 - 품사 태그
입력 시퀀스의 각 요소가 순차적으로 처리되어 대응하는 출력 시퀀스를 생성합니다. 이러한 구조는 시퀀스의 각 단계에서 개별적으로 입력과 출력을 연결하며, 모든 입력이 독립적으로 처리되는 것이 아니라, 각 시점의 은닉 상태가 이전 시점의 정보를 고려하여 출력으로 변환됩니다. POS Tagging은 입력으로 주어진 문장의 각 단어에 대해 품사를 예측하는 문제입니다. 예를 들어, 문장이 "The cat sits on the mat."이라면, 이 문장의 각 단어에 대해 그에 대응하는 품사 태그를 예측해야 합니다.
RNN 학습
순환 신경망의 원리
RNN은 현재 시점의 입력 데이터뿐만 아니라, 과거 시점의 정보를 활용하여 현재 시점의 출력 \( y_t \)를 예측합니다. 이 과정에서 사용되는 세 가지 주요 가중치 파라미터는 \( W_{xh} \), \( W_{hh} \), \( W_{hy} \)입니다.
- \( W_{xh} \): 입력 데이터 \( x_t \)를 은닉 상태로 변환하는 가중치.
- \( W_{hh} \): 이전 시점의 은닉 상태 \( h_{t-1} \)를 현재 시점의 은닉 상태로 변환하는 가중치.
- \( W_{hy} \): 은닉 상태 \( h_t \)를 출력 \( y_t \)로 변환하는 가중치.
RNN의 학습 대상 (파라미터 공유)
RNN에서 학습 대상이 되는 파라미터들은 \( W_{xh} \), \( W_{hh} \), \( W_{hy} \)입니다. 이 파라미터들은 시간 축을 따라 모든 시점에서 공유됩니다. 매 시점의 데이터를 처리할 때 동일한 파라미터가 사용되므로, 모델이 시간에 따른 패턴을 효율적으로 학습할 수 있습니다.
역전파와 가중치 업데이트
RNN은 가중치를 매 시점 적용했을 때 손실(Loss)을 최소화하는 방향으로 학습됩니다.
RNN에서의 손실(Loss)은 모델의 예측값 \( \hat {y}_t \)과 실제값 \( y_t \)의 차이로 계산되며, 이 손실을 최소화하기 위해 가중치가 업데이트됩니다.
이 과정에서 역전파(Backpropagation Through Time, BPTT) 알고리즘이 사용되며, 시간에 따라 누적된 기울기를 사용해 파라미터들을 최적화합니다.
Loss 계산하기는 RNN 학습 과정에서 매우 중요한 단계로, 모델이 얼마나 잘 예측하는지를 평가하기 위해 사용됩니다. 이를 통해 모델의 성능을 향상하기 위한 방향을 제시할 수 있습니다. 아래에 이미지를 바탕으로 Loss 계산 과정을 설명드리겠습니다.
RNN 학습 순서
1️⃣ Loss 계산하기 (Forward Propagation)
1. Forward Propagation을 통한 Loss 계산
RNN은 입력 데이터 \( x_t \)를 받아 은닉 상태 \( h_t \)를 계산하고, 이를 통해 출력값 \( \hat {y_t} \)를 예측합니다.
이 예측된 출력값 \( \hat{y_t} \)는 실제 값 \( y_t \)와 비교되어 Loss가 계산됩니다. 이때, Loss는 일반적으로 교차 엔트로피(Cross-Entropy)나 평균 제곱 오차(MSE)와 같은 함수로 계산됩니다.
Forward Propagation은 이 과정을 순차적으로 수행하며, 각 시점에서의 Loss를 계산합니다.
2. 각 시점에서의 Loss 합산
RNN의 특성상, Loss는 각 시점에서의 예측과 실제 값 간의 차이를 모두 고려합니다.
만약 출력이 다수의 시점에서 발생하는 Many-to-Many 구조나 One-to-Many 구조의 경우, 각 시점의 Loss를 평균 내어 최종 Loss로 사용합니다.

2️⃣ Gradient 계산하기 (Backward Propagation)
✅ \( W_{hy} \)에 대한 미분
1. 손실 함수(Loss)와 출력
Forward Propagation 과정에서 출력값 \( \hat {y}_t \)는 실제 값 \( y_t \)와 비교되어 손실 \( L_t \)가 계산됩니다. 이 손실에 대한 Gradient를 계산하기 위해 Backward Propagation을 적용합니다.
2. 미분을 통한 \( W_{hy} \)의 Gradient 계산
가중치 \( W_{hy} \)는 은닉 상태 \( h_t \)와 출력 \( \hat{y}_t \)를 연결하는 가중치입니다. 이 가중치에 대한 Gradient는 Loss \( L_t \)가 어떻게 \( W_{hy} \)에 의해 영향을 받는지 측정하는 값입니다. 이를 수식으로 나타내면 다음과 같습니다.
\[
\frac {\partial Loss}{\partial W_{hy}} = \frac{\partial L_t}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial W_{hy} h_t} \times \frac{\partial W_{hy} h_t}{\partial W_{hy}}
\]
위 수식에서 알 수 있듯이, Loss에 대한 미분 값은 예측값 \( \hat{y}_t \)와 은닉 상태 \( h_t \)를 고려하여 계산됩니다.
✅ \( W_{hh} \)에 대한 미분
\( W_{hh} \)에 대한 기울기 \( \frac{\partial Loss}{\partial W_{hh}} \)는 각 시점에서 누적되어 계산됩니다. 이때, 각각의 시점에서 계산된 Loss가 이전 시점들의 은닉 상태에 의해 전파되므로, 각 시간에 따른 기울기들이 모두 고려됩니다.
다음과 같은 단계로 이루어집니다.
시점 \( t_3 \)
- 시점 \( t_3 \)에서의 손실에 대한 기울기는 예측값 \( \hat{y}_t \), 은닉 상태 \( h_3 \), 그리고 \( W_{hh} \)에 의한 영향을 받습니다.
\[
\frac{\partial Loss}{\partial W_{hh}} = \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial W_{hh}}
\]
시점 \( t_2 \)
- 시점 \( t_3 \)에서의 기울기가 \( t_2 \)로 전파되며, 이를 누적합니다. \( t_2 \)에서의 은닉 상태가 \( t_3 \)에도 영향을 미치므로 \( h_2 \)에서 발생한 기울기 역시 \( W_{hh} \)에 영향을 줍니다.
\[
\frac{\partial Loss}{\partial W_{hh}} = \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial W_{hh}}
\]
시점 \( t_1 \)
- 같은 방식으로, 시점 \( t_3 \)에서 발생한 손실이 시점 \( t_1 \)까지 전파되며, 이를 모두 누적하여 \( W_{hh} \)에 대한 전체 기울기가 계산됩니다.
\[
\frac{\partial Loss}{\partial W_{hh}} = \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial h_1} \times \frac{\partial h_1}{\partial W_{hh}}
\]
3개의 시점에서의 기울기 합산
\[
\frac{\partial Loss}{\partial W_{hh}} = \left( \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial W_{hh}} \right)
+ \left( \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial W_{hh}} \right)
+ \left( \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial h_1} \times \frac{\partial h_1}{\partial W_{hh}} \right)
\]
위 식이 모든 시점에서의 기울기를 누적한 결과입니다.
위의 수식에서 볼 수 있듯이, 기울기 계산은 시간을 거슬러 올라가며 누적됩니다. 즉, 각 시점에서의 손실이 이전 시점으로 전달되며, 각 은닉 상태와 가중치 \( W_{hh} \)에 대한 영향을 계속해서 반영합니다. 중요한 점은, 모든 시점에서 발생한 기울기들을 최종적으로 합산하여 \( W_{hh} \)를 업데이트한다는 것입니다. (모든 시점에서의 손실 기여도를 고려)
✅ \( W_{xh} \)에 대한 미분 (\( W_{hh} \)와 동일)
\( W_{xh} \)에 대한 기울기 \( \frac{\partial Loss}{\partial W_{xh}} \)는 각 시점에서 누적되어 계산됩니다. 이는 은닉 상태 \( h_t \)가 입력 \( x_t \)와 \( W_{xh} \) 가중치에 의존하기 때문에, 각각의 시점에서 계산된 Loss가 이전 시점들의 은닉 상태와 입력에 의해 전파되며, 각 시간에 따른 기울기들이 모두 고려됩니다.
시점 \( t_3 \)
- 시점 \( t_3 \)에서의 손실에 대한 기울기는 예측값 \( \hat{y}_t \), 은닉 상태 \( h_3 \), 그리고 \( W_{xh} \)에 의한 영향을 받습니다. 입력 \( x_3 \)와 \( W_{xh} \) 사이의 관계가 이 시점에서 고려됩니다.
\[
\frac{\partial Loss}{\partial W_{xh}} = \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial W_{xh}}
\]
시점 \( t_2 \)
- 시점 \( t_3 \)에서의 기울기가 \( t_2 \)로 전파되며, 이를 누적합니다. \( t_2 \)에서의 은닉 상태가 \( t_3 \)에도 영향을 미치므로 \( h_2 \)에서 발생한 기울기 역시 \( W_{xh} \)에 영향을 줍니다. 이때, 입력 \( x_2 \)도 고려되어야 합니다.
\[
\frac{\partial Loss}{\partial W_{xh}} = \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial W_{xh}}
\]
시점 \( t_1 \)
- 시점 \( t_3 \)에서 발생한 손실이 시점 \( t_1 \)까지 전파되며, 이를 모두 누적하여 \( W_{xh} \)에 대한 전체 기울기가 계산됩니다. 이때 입력 \( x_1 \)도 포함됩니다.
\[
\frac{\partial Loss}{\partial W_{xh}} = \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial h_1} \times \frac{\partial h_1}{\partial W_{xh}}
\]
3개의 시점에서의 기울기 합산
\[
\frac{\partial Loss}{\partial W_{xh}} = \left( \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial W_{xh}} \right)
+ \left( \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial W_{xh}} \right)
+ \left( \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial h_1} \times \frac{\partial h_1}{\partial W_{xh}} \right)
\]
위의 수식에서 볼 수 있듯이, \( W_{xh} \) 도 \( W_{hh} \)와 마찬가지로 기울기 계산은 시간을 거슬러 올라가며 누적됩니다.
3️⃣ RNN에서의 가중치 업데이트 과정
1. RNN에서의 학습 대상
\( W_{xh} \), \( W_{hh} \), \( W_{hy} \)
이 세 가지 가중치는 각 시점의 역전파를 통해 계산된 기울기를 기반으로 업데이트됩니다.
2. 학습률 \( \eta \) (learning rate)
- 학습률 \( \eta \)는 기울기를 얼마나 반영할지를 결정하는 중요한 매개변수입니다. 일반적으로 \( \eta \) 값은 작게 설정하며, 이 슬라이드에서는 예로 \( \eta = 0.01 \)을 들고 있습니다.
- 학습률이 너무 크면 학습이 불안정해지고, 너무 작으면 학습이 느려지게 됩니다.
3. 각 가중치의 업데이트 공식
✅ \( W_{hy} \)의 업데이트
- 출력 가중치 \( W_{hy} \)에 대한 기울기 \( \frac {\partial Loss}{\partial W_{hy}} \)가 계산된 후, 이를 이용하여 새로운 \( W_{hy} \) 값을 업데이트합니다.
\[
W_{hy}^{new} = W_{hy}^{old} - \eta \times \frac{\partial Loss}{\partial W_{hy}}
\]
이는 현재의 가중치 \( W_{hy}^{old} \)에서 기울기와 학습률을 곱한 값을 빼는 방식으로, 손실을 줄이는 방향으로 업데이트합니다.
✅ \( W_{hh} \)의 업데이트
- 은닉 상태 간의 가중치 \( W_{hh} \)도 같은 방식으로 업데이트됩니다.
\[
W_{hh}^{new} = W_{hh}^{old} - \eta \times \frac{\partial Loss}{\partial W_{hh}}
\]
이는 이전 은닉 상태와의 관계에서 발생한 기울기를 반영하여 \( W_{hh} \)를 조정하는 방식입니다.
✅ \( W_{xh} \)의 업데이트
- 입력과 은닉 상태 간의 가중치 \( W_{xh} \)도 비슷하게 업데이트됩니다.
\[
W_{xh}^{new} = W_{xh}^{old} - \eta \times \frac{\partial Loss}{\partial W_{xh}}
\]
이는 입력 \( x_t \)와 은닉 상태 \( h_t \) 사이에서 계산된 기울기를 학습률에 맞춰 적용하여 \( W_{xh} \)를 업데이트하는 방식입니다.
4. 결론
각 가중치에 대한 기울기를 구한 후, 학습률을 곱한 만큼 기존의 가중치에서 빼주는 방식으로 가중치가 업데이트되며, 이 과정이 여러 번 반복되면서 RNN은 점차 더 나은 예측을 할 수 있게 됩니다.
\( W_{xh} \) , \( W_{hh} \) , \( W_{hy} \) 수식 정리
\[
\frac {\partial Loss}{\partial W_{hy}} = \frac{\partial L_t}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial W_{hy} h_t} \times \frac{\partial W_{hy} h_t}{\partial W_{hy}}
\]
\[
\frac{\partial Loss}{\partial W_{hh}} = \sum_{k=0}^{t} \left( \frac{\partial L}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_t} \times \frac{\partial h_t}{\partial h_k} \times \frac{\partial h_k}{\partial W_{hh}} \right)
\]
\[
\frac{\partial Loss}{\partial W_{xh}} = \sum_{k=0}^{t} \left( \frac{\partial L}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_t} \times \frac{\partial h_t}{\partial h_k} \times \frac{\partial h_k}{\partial W_{xh}} \right)
\]
손실 함수 종류
- 회귀 문제에서는 MSE(Mean Squared Error, 평균 제곱 오차) 손실 함수를 사용합니다.
\[
MSE = \frac {1}{N} \sum_{i=1}^{N} (y_i - \hat {y}_i)^2
\]
- 분류 문제에서는 교차 엔트로피(Cross Entropy) 손실 함수를 사용합니다.
\[
Cross Entropy = - \sum_{c=1}^{M} y_{o, c} \log(p_{o, c})
\]
여기서 \( y_{o, c} \)는 실제 클래스 값이고, \( p_{o, c} \)는 예측된 확률입니다.
Pytorch 로 RNN 구현
import torch
import torch.nn as nn
# 시드 설정
torch.manual_seed(42)
# 입력 크기 설정
d = 4 # 입력 x_t의 크기 (벡터 차원)
Dh = 6 # 은닉 상태 크기
# 1. 현재 시점 입력 데이터 생성
x_t = torch.randn(d)
print(f"x_t (현재 시점 입력) : {x_t}")
print(f"x_t 형태 : {x_t.shape}\n")
# 2. 이전 시점 은닉 상태 초기화
h_t_minus_1 = torch.zeros(1, Dh)
print(f"h_t_minus_1 (이전 시점 은닉 상태) : {h_t_minus_1}")
print(f"h_t_minus_1 형태 : {h_t_minus_1.shape}\n")
# 3. 가중치 및 편향 정의
Wxh = torch.randn(Dh, d) # 입력 가중치
Whh = torch.randn(Dh, Dh) # 은닉 상태 가중치
b = torch.randn(Dh) # 편향
print(f"Wxh (입력 가중치) 형태 : {Wxh.shape}")
print(f"Whh (은닉 상태 가중치) 형태 : {Whh.shape}")
print(f"b (편향) 형태 : {b.shape}\n")
# 4. 은닉 상태 계산
h_t = torch.tanh(
torch.matmul(x_t.unsqueeze(0), Wxh.t()) # (1, 4) x (4, 6) -> (1, 6)
+ torch.matmul(h_t_minus_1, Whh.t()) # (1, 6) x (6, 6) -> (1, 6)
+ b.unsqueeze(0) # (1, 6)
)
print(f"h_t (현재 시점 은닉 상태) : {h_t}")
print(f"h_t 형태 : {h_t.shape}\n")
# 5. 출력층 계산
Dy = 2 # 출력 크기
Why = torch.randn(Dh, Dy) # 출력 가중치
y_t = torch.sigmoid(torch.matmul(h_t, Why)) # (1, 6) x (6, 2) -> (1,2)
# 6. 최종 출력
print(f"y_t (최종 출력) : {y_t}")
print(f"y_t 형태 : {y_t.shape}")RNN의 내부 구조를 구현한 사용자 정의 RNN
import torch
import torch.nn as nn
# SimpleRNN 클래스 정의
class MyRNNcell(nn.Module):
def __init__(self, input_size, hidden_size): # 4, 6
super(MyRNNcell, self).__init__()
self.hidden_size = hidden_size
self.Wx = nn.Parameter(torch.randn(hidden_size, input_size)) # (6, 4)
self.Wh = nn.Parameter(torch.randn(hidden_size, hidden_size)) # (6, 6)
self.b = nn.Parameter(torch.randn(hidden_size)) # (6, )
def forward(self, x, hidden):
hidden = torch.tanh(torch.matmul(x, self.Wx.t()) + torch.matmul(hidden, self.Wh.t()) + self.b)
return hidden
# MyRNN 클래스 정의
class MyRNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(MyRNN, self).__init__()
self.hidden_size = hidden_size # 6
self.rnn_cell = MyRNNcell(input_size, hidden_size)
self.Wy = nn.Parameter(torch.randn(output_size, hidden_size)) # (2, 6)
def init_hidden(self, batch_size=1):
return torch.zeros(batch_size, self.hidden_size)
def forward(self, x):
h_t = self.init_hidden(x.size(0)) # 초기 은닉층
for i in range(x.size(1)): # Iterate over sequence
h_t = self.rnn_cell(x[:, i], h_t) # MyRNNcell 클래스의 forward 함수 실행 -> 이전 hidden 값 게산
output = torch.sigmoid(torch.matmul(h_t, self.Wy.t())) # Sigmoid activation
return output, h_t
sequence_data = torch.tensor([
[0.1, 0.2, 0.3, 0.4],
[0.2, 0.3, 0.4, 0.5],
[0.3, 0.4, 0.5, 0.6],
[0.4, 0.5, 0.6, 0.7],
[0.5, 0.6, 0.7, 0.8],
])
# MyRNN 모델 인스턴스화
input_size = 4 # 입력 피처의 개수
hidden_size = 6 # 은닉 상태의 크기
output_size = 1 # 출력 크기
model_myrnn1 = MyRNN(input_size, hidden_size, output_size)
# 모델을 통해 시퀀스 데이터 처리
output, ht = model_myrnn1(sequence_data.unsqueeze(0))
print("입력 시퀀스:", sequence_data)
print(f"모델 출력:, {output} {ht}")Pytorch 내장 모듈을 사용한 간단한 RNN 구현
import torch
import torch.nn as nn
class StandardRNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(StandardRNN, self).__init__()
self.hidden_size = hidden_size
self.rnn = nn.RNN(input_size, hidden_size, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
h0 = torch.zeros(1, x.size(0), self.hidden_size).to(x.device)
out, hn = self.rnn(x, h0)
out = self.fc(out[:, -1, :])
out = self.sigmoid(out)
return out, hn
# 모델 초기화
input_size = 4
hidden_size = 6
output_size = 1
model = StandardRNN(input_size, hidden_size, output_size)
# 입력 데이터
sequence_data = torch.tensor([
[0.1, 0.2, 0.3, 0.4],
[0.2, 0.3, 0.4, 0.5],
[0.3, 0.4, 0.5, 0.6],
[0.4, 0.5, 0.6, 0.7],
[0.5, 0.6, 0.7, 0.8],
]).unsqueeze(0) # 배치 차원 추가
# 모델 실행
output, hn = model(sequence_data)
print("입력 시퀀스:", sequence_data.squeeze(0))
print(f"모델 출력: {output}, 최종 은닉 상태: {hn}")'pytorch' 카테고리의 다른 글
| [pytorch] 토큰화 | 토크나이저(Tokenization) (4) | 2024.10.31 |
|---|---|
| [pytorch] LSTM(Long Short-Term Memory)이란? / LSTM을 Pytorch로 구현 실습 코드 (2) | 2024.09.26 |
| [pytorch] 과적합 방지를 위한 가중치 규제(Weight Regularization)(feat. L1 라쏘 규제, L2 릿지 규제) (0) | 2024.05.13 |
| [pytorch] Learning Rate Scheduler (학습률 동적 변경) (0) | 2024.05.03 |
| [pytorch] RNN 계층 구현하기 (0) | 2023.07.11 |