앞에서 RSS를 최소로 하는 w0,w1 (회귀 계수)를 학습을 통해서 찾는 것이 회귀의 핵심 이라고 설명하였는데
* 그렇다면 어떻게 비용함수가 최소가 되는 W 파라미터를 어떻게 구할 수 있을까?
=> 경사하강법을 이용한다.
# 경사하강법
: '점진적으로' 반복적인 계산을 통해 W 파라미터 값을 업데이트하면서 오류 값이 최소가 되는 W 파라미터를 구하는 방식

* RSS(w0,w1) 를 미분해서 미분 함수의 최솟값을 구해야 하는데, RSS(w0,w1) 는 두 개의 W 파라미터인 w0,w1을 각각 가지고 있기 때문에 w0,w1 각 변수에 편미분을 적용해야 함

# 새로운 w를 업데이트 하는 식
새로운 w0 = (이전w0) - (w0의 편미분 결괏값)
새로운 w1 = (이전w1) - (w1의 편미분 결괏값)
# 경사 하강법의 일반적인 과정
1. w0,w1를 임의의 값으로 설정한 후 첫 비용 함수의 값을 계산함
2. w0 과 w1을 새로운 w로 업데이트한 후 다시 비용 함수의 값을 계산함
3. 비용 함수의 값이 감소했으면 다시 2번을 반복. 더 이상 비용함수의 값이 감소하지 않으면 그때의 w0,w1을 구하고 반복을 중지함.
# 경사 하강법
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(0)
X = 2 * np.random.rand(100,1) # random 값은 Noise를 위해 생성
y = 6 +4 * X+np.random.randn(100,1) # y = 4X + 6 식을 근사(w1=4, w0=6).
# w1 과 w0 를 업데이트 할 w1_update, w0_update를 반환하는 함수 생성
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
N = len(y)
# w1_update, w0_update를 각각 w1, w0의 shape와 동일한 크기를 가진 0 값으로 초기화
w1_update = np.zeros_like(w1) # array([[0.]])
w0_update = np.zeros_like(w0) # array([[0.]]) # 실제 - 예측
y_pred = np.dot(X, w1.T) + w0 # 예측 배열 계산
diff = y-y_pred # 실제 - 예측
# w0_update를 dot 행렬 연산으로 구하기 위해 (값들을 합하기 위해서) 모두 1값을 가진 행렬 생성
w0_factors = np.ones((N,1))
# w1과 w0을 업데이트할 w1_update와 w0_update 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
return w1_update, w0_update
# 경사 하강 방식으로 반복적으로 수행하여 w1,w0를 업데이트하는 함수를 생성
def gradient_descent_steps(X, y, iters=10000): # iters의 횟수만큼 반복적으로 w1과 w0를 업데이트
w0 = np.zeros((1,1)) # array([[0.]]) # w0와 w1을 모두 0으로 초기화.
w1 = np.zeros((1,1)) # array([[0.]]) # w0와 w1을 모두 0으로 초기화.
# iters 만큼 반복적으로 get_weight_updates() 호출하여 w1, w0 업데이트 .
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
# RSS를 계산하는 함수
def get_cost(y,y_pred):
N=len(y)
cost=np.sum(np.square(y-y_pred))/N # np.square : 제곱
return cost
w1, w0 = gradient_descent_steps(X, y, iters=1000)
print("w1:{0:.3f} w0:{1:.3f}".format(w1[0,0], w0[0,0]))
y_pred = w1[0,0] * X + w0
print('Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))
plt.scatter(X, y) #실제 그래프 ( 점 )
plt.plot(X,y_pred) # 예측 그래프 ( 선 )w1:4.022 w0:6.162
Gradient Descent Total Cost:0.9935
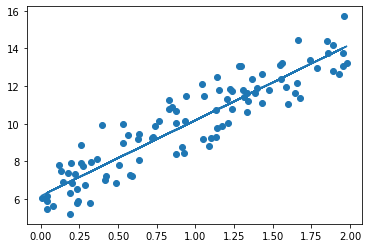
* 경사 하강법은 모든 학습 데이터에 대해 반복적으로 비용함수 최소화를 위한 값을 업데이트하기 때문에 수행 시간이 매우 오래 걸린다는 단점이 있다.
반면 확률적 경사 하강법은 일부 데이터만 이용해 W가 업데이트되는 값을 계산하기 때문에 경사하강법에 비해 빠른 속도를 보장한다. ( 실전에서 주로 사용)
# 확률적 경사 하강법
def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=1000):
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
prev_cost = 100000
iter_index =0
for ind in range(iters):
np.random.seed(ind)
stochastic_random_index = np.random.permutation(X.shape[0]) # 100개(X.shape[0])의 숫자를 랜덤으로 추출
sample_X = X[stochastic_random_index[0:batch_size]] # 전체 X 데이터에서 랜덤하게 batch_size만큼 데이터 추출하여 sample_X로 저장
sample_y = y[stochastic_random_index[0:batch_size]] # 전체 y 데이터에서 랜덤하게 batch_size만큼 데이터 추출하여 sample_y로 저장
# 랜덤하게 batch_size만큼 추출된 데이터로 w1_update, w0_update 계산 후 업데이트
w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
w1, w0 = stochastic_gradient_descent_steps(X, y, iters=1000)
print("w1:",round(w1[0,0],3),"w0:",round(w0[0,0],3))
y_pred = w1[0,0] * X + w0
print('Stochastic Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))w1: 4.028 w0: 6.156
Stochastic Gradient Descent Total Cost:0.9937* 확률적 경사 하강법과 경사 하강법으로 구한 w1,w0가 별 차이가 없고, 예측 오류 또한 예측 성능상의 차이가 없다.
따라서 큰 데이터를 처리할 경우에는 일반적으로 확률적 경사 하강법을 이용한다.
'pythonML' 카테고리의 다른 글
| [pythonML] 정확도와 오차행렬 - 평가 (0) | 2022.07.10 |
|---|---|
| [pythonML] 회귀- LinearRegression (0) | 2022.05.09 |
| [pythonML] 회귀 - 단순 선형 회귀 (0) | 2022.04.17 |
| [pythonML] 부스팅(Boosting)- XGBoost(eXtra Gradient Boost) (0) | 2022.04.04 |
| [pythonML] 부스팅(Boosting) - GBM /AdaBoost (0) | 2022.04.01 |